
分析 首先由由f(x-1)的图象关于(1,0)中心对称知f(x)的图象关于(0,0)中心对称,根据奇函数定义与减函数性质得出s与t的关系式,然后利用线性规划的知识即可求得结果.
解答  解:把函数y=f(x)向右平移1个单位可得函数y=f(x-1)的图象
解:把函数y=f(x)向右平移1个单位可得函数y=f(x-1)的图象
∵函数y=f(x-1)得图象关于(1,0)成中心对称
∴函数y=f(x)的图象关于(0,0)成中心对称,即函数y=f(x)为奇函数
∵f(s2-2s)≤-f(2t-t2)=f(t2-2t)且函数y=f(x)在R上单调递减
∴s2-2s≥t2-2t在s∈[1,4]上恒成立
即(t-s)(s+t-2)≤0
∵1≤s≤4
∴-2≤2-s≤1,即2-s≤s
∴2-s≤t≤s
作出不等式所表示的平面区域,如图的阴影部分的△ABC,C(4,-2),A(1,1),B(4,4).
∴s-2t在B(4,4)处取得最小值-4.
故答案为:-4.
点评 本题综合考查函数的奇偶性、单调性知识,同时考查由最大值、最小值求取值范围的策略,以及运算能力,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 16π | C. | $\frac{16π}{3}$ | D. | $\frac{32π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
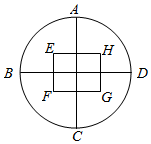 如图所示是外框为圆形的一种图标.已知圆的半径为60mm,A,B,C,D是圆周的四等分点,圆内框架总长是360mm,设计要求是:矩形EFGH的周长与面积的比值最小.试问矩形EFGH的长与宽各是多少mm时符合设计要求.此时的比值是多少?
如图所示是外框为圆形的一种图标.已知圆的半径为60mm,A,B,C,D是圆周的四等分点,圆内框架总长是360mm,设计要求是:矩形EFGH的周长与面积的比值最小.试问矩形EFGH的长与宽各是多少mm时符合设计要求.此时的比值是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 480 | B. | 960 | C. | 720 | D. | 180 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com