

| A. | $\frac{π}{3}$ | B. | $arcsin\frac{{\sqrt{6}}}{3}$ | C. | $\frac{π}{6}$ | D. | $arcsin\frac{{2\sqrt{39}}}{13}$ |
分析 由三视图画出对应直观图,根据正三棱锥的结构特征判断出顶点V在底面上的射影,由图象和正三角形的特征求出侧棱在底面上的射影,根据线面成角的定义判断出侧棱与底面所成的角,由余弦函数求出此角的余弦值,由特殊角的三角函数值求出此角的大小.
解答  解:由三视图画出直观图如图所示:
解:由三视图画出直观图如图所示:
O是顶点V在底面的射影,且O是正三角形ABC的中心,D是BC的中点,
由三视图可得,侧棱VA=4,AB=BC=AC=2$\sqrt{3}$,
∴底面△ABC外接圆的半径OA=$\frac{2}{3}AD$=$\frac{2}{3}×\sqrt{(2\sqrt{3})^{2}-(\sqrt{3})^{2}}$=2
∴侧棱在底面上的射影A0=2,
由线面成角的定义可知该正三棱锥侧棱与底面所成的角是∠VAO,
∴$cos∠VAO=\frac{2}{4}=\frac{1}{2}$,则三棱锥侧棱与底面所成的角为$\frac{π}{3}$,
故选:A.
点评 本题考查正三棱锥的三视图、结构特征的应用,线面成角的定义,正确画出直观图是解题的关键,考查空间想象能力和数形结合思想.


 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相切 | C. | 相交且过圆心 | D. | 相交但不过圆心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
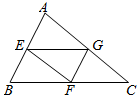 如图,在△ABC中,AB=2$\sqrt{5}$,BC=2$\sqrt{10}$,AC=2$\sqrt{13}$,E、F、G分别为三边中点,将△BEF,△AEG,△GCF分别沿EF、EG、GF向上折起,使A、B、C重合,记为S,则三棱锥S-EFG的外接球面积为( )
如图,在△ABC中,AB=2$\sqrt{5}$,BC=2$\sqrt{10}$,AC=2$\sqrt{13}$,E、F、G分别为三边中点,将△BEF,△AEG,△GCF分别沿EF、EG、GF向上折起,使A、B、C重合,记为S,则三棱锥S-EFG的外接球面积为( )| A. | 14π | B. | 15π | C. | $\frac{29}{2}$π | D. | 2$\sqrt{33}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{6}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m>n | B. | m<n | C. | m=n | D. | m≤n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 16π | C. | $\frac{16π}{3}$ | D. | $\frac{32π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
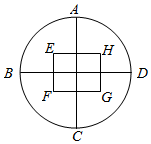 如图所示是外框为圆形的一种图标.已知圆的半径为60mm,A,B,C,D是圆周的四等分点,圆内框架总长是360mm,设计要求是:矩形EFGH的周长与面积的比值最小.试问矩形EFGH的长与宽各是多少mm时符合设计要求.此时的比值是多少?
如图所示是外框为圆形的一种图标.已知圆的半径为60mm,A,B,C,D是圆周的四等分点,圆内框架总长是360mm,设计要求是:矩形EFGH的周长与面积的比值最小.试问矩形EFGH的长与宽各是多少mm时符合设计要求.此时的比值是多少?查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com