
分析 设抛物线y2=2px(p>0)的准线为l,分别过点A,B作AM⊥l,BN⊥l,垂足为M,N.过点B作BC⊥AM交于点C.由抛物线的定义可得:|AM|=|AF|,|BN|=|BF|.由于AM∥x轴,∠BAC=∠AFx=60°.在Rt△ABC中,|AC|=$\frac{1}{2}$|AB|,化简即可得出.
解答 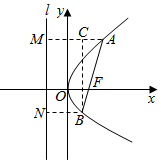 解:斜率为$\sqrt{3}$的直线倾斜角为60°.
解:斜率为$\sqrt{3}$的直线倾斜角为60°.
设抛物线y2=2px(p>0)的准线为l:x=-$\frac{p}{2}$.
如图所示,分别过点A,B作AM⊥l,BN⊥l,垂足为M,N.
过点B作BC⊥AM交于点C.
则|AM|=|AF|,|BN|=|BF|.
∵AM∥x轴,
∴∠BAC=∠AFx=60°.
在Rt△ABC中,|AC|=$\frac{1}{2}$|AB|
又|AM|-|BN|=|AC|,
∴|AF|-|BF|=$\frac{1}{2}$(|AF|+|BF|),
化为|AF|=3|BF|,则$\frac{{|{AF}|}}{{|{BF}|}}$=3.
故答案为:3.
点评 本题考查了抛物线的定义、含60°角的直角三角形的性质、平行线的性质,考查了辅助线的作法,属于中档题.


科目:高中数学 来源: 题型:选择题

| A. | $\frac{π}{3}$ | B. | $arcsin\frac{{\sqrt{6}}}{3}$ | C. | $\frac{π}{6}$ | D. | $arcsin\frac{{2\sqrt{39}}}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-4,1) | B. | (-1,1) | C. | (-∞,-4)∪(1,+∞) | D. | (-4,-1)∪(-1,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题P:?x0∈R,x02-x0+1<0,则¬P:?x∉R,x2-x+1≥0 | |
| B. | 命题“若圆C:(x-m+1)2+(y-m)2=1与两坐标轴都有公共点,则实数m∈[0,1]”的逆否命题为真命题 | |
| C. | 已知相关变量(x,y)满足回归方程$\widehat{y}$=2-3x,若变量x增加一个单位,则y平均增加3个单位 | |
| D. | 已知随机变量X~N(2,σ2),若P(X<a)=0.32,则P(X>4-a)=0.68 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. |  | B. | 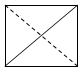 | C. | 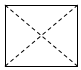 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$-cos1 | B. | $\frac{10}{3}$-cos1 | C. | $\frac{7}{3}$+cos1 | D. | $\frac{10}{3}$+cos1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com