
| A. | 若命题P:?x0∈R,x02-x0+1<0,则¬P:?x∉R,x2-x+1≥0 | |
| B. | 命题“若圆C:(x-m+1)2+(y-m)2=1与两坐标轴都有公共点,则实数m∈[0,1]”的逆否命题为真命题 | |
| C. | 已知相关变量(x,y)满足回归方程$\widehat{y}$=2-3x,若变量x增加一个单位,则y平均增加3个单位 | |
| D. | 已知随机变量X~N(2,σ2),若P(X<a)=0.32,则P(X>4-a)=0.68 |
分析 A.根据特称命题的否定是全称命题进行判断即可
B.求出圆心坐标,根据圆心坐标,得到圆心到x,y轴的距离与半径的关系进行求解即可.
C.根据线性回归方程的性质进行判断.
D.根据正态分布的性质,利用对称性进行求解即可.
解答 解:A.命题是特称命题,则命题的否定是全称命题,则¬P:?x∈R,x2-x+1≥0,故A错误,
B.由圆的标准方程得圆心坐标C(m-1,m),半径R=1,
若圆C:(x-m+1)2+(y-m)2=1与两坐标轴都有公共点,
则$\left\{\begin{array}{l}{|m|≤1}\\{|m-1|≤1}\end{array}\right.$,即$\left\{\begin{array}{l}{-1≤m≤1}\\{-1≤m-1≤1}\end{array}\right.$,即$\left\{\begin{array}{l}{-1≤m≤1}\\{0≤m≤2}\end{array}\right.$,
则0≤m≤1,即实数m的取值范围是[0,1],故原命题为真命题,则命题的逆否命题为真命题,故B正确
C.相关变量(x,y)满足回归方程$\widehat{y}$=2-3x,若变量x增加一个单位,则y平均减少3个单位,故C错误,
D.∵随机变量X服从正态分布N(2,σ2),μ=2,
∴关于x=2对称,
∴P(x<a)=P(x>4-a)=0.32.故D错误,
故选:B
点评 本题主要考查命题的真假判断,涉及的知识点较多,综合性较强,但难度不大.


 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 16π | C. | $\frac{16π}{3}$ | D. | $\frac{32π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
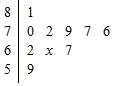 高三某班级10名同学的物理期中考试成绩分布的茎叶图如图,其中一名同学的成绩有误,其末位数记为x,已知这10名学生成绩的中位数与平均数相同,则x的值为( )
高三某班级10名同学的物理期中考试成绩分布的茎叶图如图,其中一名同学的成绩有误,其末位数记为x,已知这10名学生成绩的中位数与平均数相同,则x的值为( )| A. | 3 | B. | 5 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com