
分析 (1)求出φ(x)的表达式,通过讨论x的范围,求出φ(x)的单调区间,求出其最大值即可;(2)通过讨论x的范围,求出不等式的解集即可.
解答 解:(1)∵f(x+1)=x,∴f(x)=x-1,
∵函数g(x)=-x2+ax-b,且不等式g(x)≤0的解集是(-∞,1]∪[5,+∞),
∴-x2+ax-b≤0即x2-ax+b≥0的解集是(-∞,1]∪[5,+∞),
∴a=6,b=5,
∴g(x)=-x2+6x-5,
∴φ(x)=g(x)-|f(x)|=-x2+6x-5-|x-1|,
x≥1时,φ(x)=-x2+5x-4,对称轴x=$\frac{5}{2}$,
∴φ(x)在[1,$\frac{5}{2}$)递增,在($\frac{5}{2}$,+∞)递减,
∴φmax(x)=φ($\frac{5}{2}$)=$\frac{9}{4}$,
x<1时,φ(x)=-x2+7x-6,对称轴x=$\frac{7}{2}$,
∴φ(x)在(-∞,1)递增,
∴φmax(x)=φ(1)=0,
综上,φmax(x)=φ($\frac{5}{2}$)=$\frac{9}{4}$;
(2)x≥1时,-x2+6x-5≥x-1,解得:1≤x≤4,
x<1时,-x2+6x-5≥-x+1,解得:1≤x≤6,舍,
综上,不等式g(x)≥|f(x)|的解集是[1,4].
点评 本题考查了二次函数的性质,考查绝对值不等式问题,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | (2,5) | B. | [2,5] | C. | (2,5] | D. | [2,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相切 | C. | 相交且过圆心 | D. | 相交但不过圆心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2k-1 | B. | 2k-1 | C. | 2k | D. | 2k+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16π | B. | 32π | C. | 64π | D. | 128π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
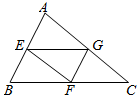 如图,在△ABC中,AB=2$\sqrt{5}$,BC=2$\sqrt{10}$,AC=2$\sqrt{13}$,E、F、G分别为三边中点,将△BEF,△AEG,△GCF分别沿EF、EG、GF向上折起,使A、B、C重合,记为S,则三棱锥S-EFG的外接球面积为( )
如图,在△ABC中,AB=2$\sqrt{5}$,BC=2$\sqrt{10}$,AC=2$\sqrt{13}$,E、F、G分别为三边中点,将△BEF,△AEG,△GCF分别沿EF、EG、GF向上折起,使A、B、C重合,记为S,则三棱锥S-EFG的外接球面积为( )| A. | 14π | B. | 15π | C. | $\frac{29}{2}$π | D. | 2$\sqrt{33}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com