
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{{2\sqrt{6}}}{5}$ | D. | $-\frac{{2\sqrt{6}}}{5}$ |
分析 由已知利用同角三角函数基本关系式可求cos($α+\frac{π}{4}$)的值,进而利用诱导公式化简所求即可得解.
解答 解:∵α是第二象限角,sin(α+$\frac{π}{4}$)=$\frac{1}{5}$,
∴$\frac{3π}{4}<α+\frac{π}{4}<\frac{5π}{4}$,
∴$cos(α+\frac{π}{4})=-\frac{{2\sqrt{6}}}{5}$,
∴$sin(α+\frac{3π}{4})=sin(α+\frac{π}{4}+\frac{π}{2})=cos(α+\frac{π}{4})=-\frac{{2\sqrt{6}}}{5}$.
故选:D
点评 本题主要考查了同角三角函数基本关系式,诱导公式在三角函数化简求值中的应用,属于基础题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{25}{16}$ | D. | $\frac{5}{3}$或$\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,5) | B. | [2,5] | C. | (2,5] | D. | [2,5) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2,0} | B. | {2,0} | C. | {-2,-1,0} | D. | {2,1,0} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10份 | B. | 20份 | C. | 30份 | D. | 40份 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 相离 | B. | 相切 | C. | 相交且过圆心 | D. | 相交但不过圆心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
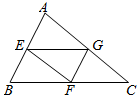 如图,在△ABC中,AB=2$\sqrt{5}$,BC=2$\sqrt{10}$,AC=2$\sqrt{13}$,E、F、G分别为三边中点,将△BEF,△AEG,△GCF分别沿EF、EG、GF向上折起,使A、B、C重合,记为S,则三棱锥S-EFG的外接球面积为( )
如图,在△ABC中,AB=2$\sqrt{5}$,BC=2$\sqrt{10}$,AC=2$\sqrt{13}$,E、F、G分别为三边中点,将△BEF,△AEG,△GCF分别沿EF、EG、GF向上折起,使A、B、C重合,记为S,则三棱锥S-EFG的外接球面积为( )| A. | 14π | B. | 15π | C. | $\frac{29}{2}$π | D. | 2$\sqrt{33}$π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com