
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{25}{16}$ | D. | $\frac{5}{3}$或$\frac{5}{4}$ |
分析 求出圆的标准方程,利用双曲线的渐近线和圆相切的等价条件建立方程得到a,b的关系即可得到结论.
解答 解:圆x2+y2-6x-2y+9=0的标准方程为(x-3)2+(y-1)2=1,
则圆心为M(3,1),半径R=1,
由mx2+ny2=0得$\frac{{y}^{2}}{\frac{1}{n}}$-$\frac{{x}^{2}}{-\frac{1}{m}}$=1,
则双曲线的焦点在y轴,则对应的渐近线为y=±$\frac{a}{b}$x,
设双曲线的一条渐近线为y=$\frac{a}{b}$x,即ax-by=0,
∵一条渐近线与圆x2+y2-6x-2y+9=0相切,
∴即圆心到直线的距离d=$\frac{|3a-b|}{\sqrt{{a}^{2}+{b}^{2}}}$=1,
即|3a-b|=c,
平方得9a2-6ab+b2=c2=a2+b2,
即8a2-6ab=0,
则4a-3b=0,
则b=$\frac{4}{3}$a,平方得b2=$\frac{16}{9}$a2=c2-a2,
即c2=$\frac{25}{9}$a2,
则c=$\frac{5}{3}$a,
则离心率e=$\frac{c}{a}$=$\frac{5}{3}$,
故选:A.
点评 本题主要考查双曲线离心率的计算,根据直线和圆相切的等价条件建立方程是解决本题的关键.考查学生的计算能力.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 地理 历史 | [80,100] | [60,80] | [40,60] |
| [80,100] | 8 | m | 9 |
| [60,80] | 9 | n | 9 |
| [40,60] | 8 | 15 | 7 |
| [80,100] | [60,80] | [40,60] | |
| 地理 | |||
| 历史 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{x}$•sinx+1=0 | B. | $\frac{1}{x}$•sinx-1=0 | C. | x•sinx+1=0 | D. | x•sinx-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (45°,90°) | B. | (45°,90°] | C. | (0,45°) | D. | (45°,60°) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{9}{16}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
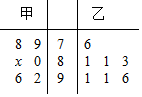 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{{2\sqrt{6}}}{5}$ | D. | $-\frac{{2\sqrt{6}}}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com