
| A. | (45°,90°) | B. | (45°,90°] | C. | (0,45°) | D. | (45°,60°) |
分析 讨论焦点在x轴上和y轴上,将椭圆、双曲线的方程化为标准方程,由基本量的关系和条件,求得n=1,-1<m<0,由双曲线的渐近线方程,可得斜率,进而得到倾斜角的范围.
解答 解:当焦点在x轴上时,由题意知:m>0,n<0,
椭圆${C_1}:\frac{x^2}{m+1}+\frac{y^2}{3-n}=1$中,$a_1^2=m+1,b_1^2=3-n$,
则$c_1^2=a_1^2-b_1^2=m+n-2$;
双曲线${C_2}:\frac{x^2}{m}-\frac{y^2}{-n}=1$中,$a_2^2=m,b_2^2=-n$,
则$c_2^2=a_2^2+b_2^2=m-n$;
由题意,m+n-2=m-n,解得n=1,这与n<0矛盾;
当焦点在y轴上时,由题意知-1<m<0,0<n<3,
椭圆${C_1}:\frac{y^2}{3-n}+\frac{x^2}{m+1}=1$中,$a_1^2=3-n,b_1^2=m+1$,
则$c_1^2=a_1^2-b_1^2=-m-n+2$;
双曲线${C_2}:\frac{x^2}{m}-\frac{y^2}{-n}=1$可化为${C_2}:\frac{y^2}{n}-\frac{x^2}{-m}=1$,$a_2^2=n,b_2^2=-m$,
则$c_2^2=a_2^2+b_2^2=n-m$;
由题意,-m-n+2=n-m,解得n=1,
双曲线C2的一条斜率为正的渐近线的斜率为$k=\frac{a_2}{b_2}=\sqrt{\frac{n}{-m}}=\sqrt{-\frac{1}{m}}$,
又因为-1<m<0,所以$-\frac{1}{m}>1$,所以$\sqrt{-\frac{1}{m}}>1$,
即双曲线C2的一条斜率为正的渐近线的倾斜角的取值范围为(45°,90°),
故选:A.
点评 本题考查双曲线的渐近线的倾斜角的范围,注意运用分类讨论的思想方法和椭圆、双曲线的基本量的关系,考查化简整理的运算能力,属于中档题.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
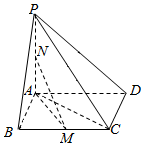 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AD=2,AB=1,AC=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AD=2,AB=1,AC=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{3}$ | B. | $\frac{5}{4}$ | C. | $\frac{25}{16}$ | D. | $\frac{5}{3}$或$\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\frac{1}{4}$ | C. | $\frac{1}{16}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6826 | B. | 3174 | C. | 228 | D. | 456 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com