练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    11．已知ABCD为矩形，AB=3，BC=2，在矩形ABCD内随机取一点P，点P到矩形四个顶点的距离都大于1的概率为1-$\frac{π}{6}$．

    分析 在矩形ABCD内随机取一点P，点P到点O的距离大于1的轨迹是以O为圆心，1为半径的$\frac{1}{4}$圆的外部，点P到矩形四个顶点的距离都大于1面积为3×2-4×$\frac{1}{4}$×π×12=6-π，求出矩形面积即可得到结果．

    解答 解：在矩形ABCD内随机取一点P，点P到点O的距离大于1的轨迹是以O为圆心，1为半径的$\frac{1}{4}$圆的外部，故点P到矩形四个顶点的距离都大于1的面积为3×2-4×$\frac{1}{4}$×π×12=6-π，
    ∵矩形ABCD的面积为3×2=6，
    ∴点P到矩形四个顶点的距离都大于1的概率为$\frac{6-π}{6}$=1-$\frac{π}{6}$．
    故答案为：1-$\frac{π}{6}$．

    点评 此题考查了几何概型，熟练掌握几何概型公式是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    1．近年来我国电子商务行业迎来篷布发张的新机遇，2015年双11期间，某购物平台的销售业绩高达918亿人民币，与此同时，相关管理部门推出了针对电商的商品和服务的评价体系，现从评价系统中选出200次成功交易，并对其评价进行统计，对商品的好评率为0.6，对服务的好评率为0.75，其中对商品和服务都做出好评的交易为80次．
    （Ⅰ）完成商品和服务评价的2×2列联表，并说明是否可以在犯错误概率不超过0.1%的前提下，认为商品好评与服务好评有关？
    （Ⅱ）若将频率视为概率，某人在该购物平台上进行的5次购物中，设对商品和服务全好评的次数为随机变量X．
    ①求对商品和服务全好评的次数X的分布列（概率用组合数算式表示）；
    ②求X的数学期望和方差．
    参考数据及公式如下：
     P（K2≥k） 0.150.10 0.05 0.025 0.010 0.005 0.001 
     k 2.0722.706 3.841 5.024 6.635 7.879 10.828 
    （K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知函数f（x）和g（x）是两个定义在区间M上的函数，若对任意的x∈M，存在常数x0∈M，使得f（x）≥f（x0），g（x）≥g（x0），且f（x）=g（x0，则称f（x）与g（x）在区间M上是“相似函数”，若f（x）=2x2+ax+b与g（x）=x+$\frac{4}{x}$在[1，$\frac{5}{2}$]上是“相似函数”，则函数f（x）在区间[1，$\frac{5}{2}$]上的最大值为（　　）
    A．4B．$\frac{9}{2}$C．6D．$\frac{89}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

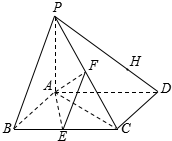    19．四棱锥P-ABCD底面是菱形，PA⊥平面ABCD，∠ABC=60°，E、F分别是BC、PC的中点．
    （Ⅰ）求证：平面AEF⊥平面PAD；
    （Ⅱ）若$\frac{PA}{AB}$=$\sqrt{3}$，设H为PD的四等分点（靠近点D），求EH与平面AEF所成角的正弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．设等比数列{an}，a1=1，a4=8，则S10=1023．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．记实数a，b中的最大数为max{a，b}，定义数列{an}：an=max{n2，2n}，则数列{an}的前10项和为（　　）
    A．2046B．2047C．2048D．2049

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    3．在平面直角坐标系xOy中，以原点O为极点，x轴的非负半轴为极轴建立极坐标系．已知曲线C1的极坐标方程为ρ=8$\sqrt{2}$cos（θ-$\frac{3π}{4}$），曲线C2的参数方程为$\left\{\begin{array}{l}{x=8cosθ}\\{y=3sinθ}\end{array}\right.$，（θ为参数）．
    （1）将曲线C1的极坐标方程化为直角坐标方程，将曲线C2的参数方程化为普通方程；
    （2）若P是曲线C2上的动点，求P到直线l：$\left\{\begin{array}{l}{x=3+2t}\\{y=-2+t}\end{array}\right.$，（t为参数）的距离的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．设数集A={-1，x1，x2，…xn}，其中0＜x1＜x2＜…＜xn，n≥2，向量集B={$\overrightarrow{a}$|$\overrightarrow{a}$=（x，y），x∈A，y∈A}．若?$\overrightarrow{{a}_{1}}$∈B，?$\overrightarrow{{a}_{2}}$∈B使得$\overrightarrow{{a}_{1}}$•$\overrightarrow{{a}_{2}}$=0，则称A具有性质P．
    （1）若a＞1，数集A={-1，1，a}，求证：数集A具有性质P；
    （2）若b＞$\sqrt{2}$，数集A={-1，1，$\sqrt{2}$，b}具有性质P，求b的值；
    （3）若数集A={-1，x1，x2，…xn}（其中0＜x1＜x2＜…＜xn，n≥2）具有性质P，x1=1，x2=q（q为常数，q＞1），求数列{xk}的通项公式xk（k∈N*，k≤n）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．已知椭圆C1：$\frac{x^2}{m+1}$+$\frac{y^2}{3-n}$=1与双曲线C2：$\frac{x^2}{m}$-$\frac{y^2}{-n}$=1有相同的焦点，则双曲线C2的一条斜率为正的渐近线的倾斜角的取值范围为（　　）
    A．（45°，90°）B．（45°，90°]C．（0，45°）D．（45°，60°）

    查看答案和解析>>

    同步练习册答案