
分析 (1)运用新定义,结合向量垂直的条件:数量积为0,即可得证;
(2)选取$\overrightarrow{{a}_{1}}$=(b,$\sqrt{2}$),A中与$\overrightarrow{{a}_{1}}$垂直的元素必有形式(-1,m).所以b=$\sqrt{2}$m,由b>$\sqrt{2}$,可由m=$\sqrt{2}$,从而b=2;
(3)先猜想结论:xk=qk-1,k=1,2,3,…,n.记Ak═{-1,x1,x2,…,xk},k=2,3,…,n,通过反证法证明出引理:若Ak+1具有性质P,则Ak也具有性质P.最后用数学归纳法,可证明出xk=qk-1,k=1,2,3,…,n.
解答 证明:(1)由A={-1,1,a},
可得$\overrightarrow{{a}_{1}}$=(m,n)∈A,设$\overrightarrow{{a}_{2}}$=(s,t)∈A,
$\overrightarrow{{a}_{1}}$•$\overrightarrow{{a}_{2}}$=ms+nt,由于A中含有-1,1,
总能使得ms+nt=0,则数集A具有性质P;
解:(2)b>$\sqrt{2}$,数集A={-1,1,$\sqrt{2}$,b}具有性质P,
选取$\overrightarrow{{a}_{1}}$=(b,$\sqrt{2}$),A中与$\overrightarrow{{a}_{1}}$垂直的元素必有形式(-1,m).
所以b=$\sqrt{2}$m,由b>$\sqrt{2}$,可由m=$\sqrt{2}$,从而b=2;
(3)猜想:xk=qk-1,k=1,2,3,…,n
记Ak═{-1,x1,x2,…,xk},k=2,3,…,n
先证明若Ak+1具有性质P,则Ak也具有性质P.
任取$\overrightarrow{{a}_{1}}$=(s,t),s、t∈Ak,当s、t中出现-1时,
显然有$\overrightarrow{{a}_{2}}$满足$\overrightarrow{{a}_{1}}$•$\overrightarrow{{a}_{2}}$=0,
当s、t中都不是-1时,满足s≥1且t≥1.
因为Ak+1具有性质P,所以有$\overrightarrow{{a}_{2}}$=(s1,t1),s1、t1∈Ak+1,
使得$\overrightarrow{{a}_{1}}$•$\overrightarrow{{a}_{2}}$=0,从而s1、t1其中有一个为-1.
不妨设s1=-1,
假设t1∈Ak+1,且t1∉Ak,则t1=xk+1.
由(s,t)(-1,xk+1)=0,得s=txk+1≥xk+1,与s∈Ak矛盾.
所以t1∈Ak,从而Ak也具有性质P.
再用数学归纳法,证明xi=qi-1,i=1,2,3,…,n
当n=2时,结论显然成立;
假设当n=k时,Ak═{-1,x1,x2,…,xk}具有性质P,则xi=qi-1,i=1,2,…,k
当n=k+1时,若Ak+1═{-1,x1,x2,…,xk+1}具有性质P,
则Ak═{-1,x1,x2,…,xk}具有性质P,
所以Ak+1═{-1,q,q2,…,qk-1,xk+1}.
取$\overrightarrow{{a}_{1}}$=(xk+1,q),并设$\overrightarrow{{a}_{2}}$=(s,t)∈Y,满足$\overrightarrow{{a}_{1}}$•$\overrightarrow{{a}_{2}}$=0,
由此可得s=-1或t=-1
若t=-1,则xk+1=$\frac{q}{s}$<q,不可能.
所以s=-1,xk+1=qt=qj≤qk且xk+1>qk-1,因此xk+1=qk
综上所述,xk=qk-1,k=1,2,3,…,n.
点评 本题以向量的数量积的坐标运算为载体,着重考查了集合元素的性质与向量的综合等知识点,本题是一道综合题,请同学们注意解题过程中的转化化归思想的运用.


科目:高中数学 来源: 题型:填空题
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BCD=135°,侧面PAB⊥底面ABCD,∠BAP=90°,AB=AC=PA=2,E,F分别为BC,AD的中点,点M在线段PD上.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
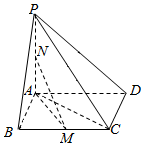 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AD=2,AB=1,AC=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AD=2,AB=1,AC=$\sqrt{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6826 | B. | 3174 | C. | 228 | D. | 456 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com