
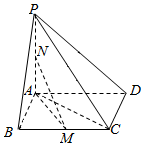
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AD=2,AB=1,AC=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,PA⊥平面ABCD,点M、N分别为BC、PA的中点,且PA=AD=2,AB=1,AC=$\sqrt{3}$.分析 (1)由PA⊥平面ABCD得PA⊥CD,由勾股定理的逆定理得出AC⊥CD,故而CD⊥平面PAC;
(2)取PD中点E,连接NE,CE即可证明四边形MNEC为平行四边形,于是MN∥CE,于是VP-ACE=VE-PAC=$\frac{1}{2}{V}_{D-PAC}$.
解答 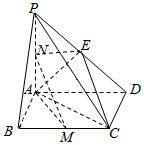 证明:(1)∵AD=2,AC=$\sqrt{3}$,CD=AB=1,
证明:(1)∵AD=2,AC=$\sqrt{3}$,CD=AB=1,
∴AC2+CD2=AD2,即AC⊥CD.
∵PA⊥平面ABCD,CD?平面ABCD,
∴PA⊥CD
又PA?平面PAC,AC?平面PAC,PA∩AC=A,
∴CD⊥平面PAC.
(2)线段PD上存在一点E,使得MN∥平面ACE.
证明:取PD中点E,连接NE,CE,AE.
∵NE是△PAD的中位线,∴NE$\stackrel{∥}{=}\frac{1}{2}AD$,又CM$\stackrel{∥}{=}\frac{1}{2}AD$,
∴NE$\stackrel{∥}{=}$MC,
∴四边形MNEC是平行四边形,
∴MN∥CE,
又CE?平面ACE,MN?平面ACE,
∴MN∥平面ACE.
即E为PD中点时,MN∥平面ACE.
∴VP-ACE=VE-PAC=$\frac{1}{2}{V}_{D-PAC}$=$\frac{1}{6}{S}_{△PAC}•CD$=$\frac{1}{6}×\frac{1}{2}×\sqrt{3}×2×1$=$\frac{\sqrt{3}}{6}$.
点评 本题考查了线面平行,线面垂直的判定,棱锥的体积计算,属于中档题.


科目:高中数学 来源: 题型:解答题
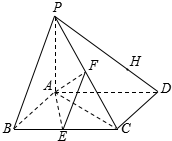 四棱锥P-ABCD底面是菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.
四棱锥P-ABCD底面是菱形,PA⊥平面ABCD,∠ABC=60°,E、F分别是BC、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 地理 历史 | [80,100] | [60,80] | [40,60] |
| [80,100] | 8 | m | 9 |
| [60,80] | 9 | n | 9 |
| [40,60] | 8 | 15 | 7 |
| [80,100] | [60,80] | [40,60] | |
| 地理 | |||
| 历史 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 24 | C. | 16 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (45°,90°) | B. | (45°,90°] | C. | (0,45°) | D. | (45°,60°) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 7-4$\sqrt{3}$ | B. | 2-$\sqrt{3}$ | C. | $\sqrt{3}$-1 | D. | 4-2$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 离散型随机变量X~B(4,0.1),则D(X)=0.4 | |
| B. | 将一组数据中的每个数据都减去同一个数后,平均值与方差均没有变化 | |
| C. | 采用系统抽样法从某班按学号抽取5名同学参加活动,学号为5,16,27,38,49的同学均被选出,则该班学生人数可能为60 | |
| D. | 某糖果厂用自动打包机打包,每包的重量X(kg)服从正态分布N(100,1.44),从该糖厂进货10000包,则重量少于96.4kg一般不超过15包 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com