
分析 首先将圆方程化成标准形式,求出圆心为(1,-3),当抛物线焦点在y轴上时,设x2=2py,将圆心代入,求出方程;当抛物线焦点在x轴上时,设y2=2px,将圆心代入,求出方程.
解答 解:圆方程x2+y2-2x+6y+9=0化为(x-1)2+(y+3)2=1,
可得圆心坐标为(1,-3),
(1)当抛物线焦点在y轴上时,设x2=2py,p=-$\frac{1}{6}$,∴x2=-$\frac{1}{3}$y;
(2)当抛物线焦点在x轴上时,设y2=2px,p=$\frac{9}{2}$,∴y2=9x.
故答案为:y2=9x或x2=$-\frac{1}{3}$y.
点评 本题考查了抛物线和圆的标准方程,但要注意抛物线的位置有在x轴和y轴两种情况,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①④⑤⑥ | B. | ②④⑤ | C. | ③④⑤⑥ | D. | ①⑤⑥ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 地理 历史 | [80,100] | [60,80] | [40,60] |
| [80,100] | 8 | m | 9 |
| [60,80] | 9 | n | 9 |
| [40,60] | 8 | 15 | 7 |
| [80,100] | [60,80] | [40,60] | |
| 地理 | |||
| 历史 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
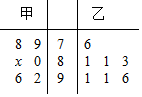 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com