
分析 通过并项相加可知当n≥2时an-a1=2[n+(n-1)+…+3+2],进而可得数列{an}的通项公式an=n(n+1),裂项、并项相加可知bn=$\frac{1}{2n+\frac{1}{n}+3}$,通过求导可知$f(x)=2x+\frac{1}{x}(x≥1)$是增函数,进而问题转化为${t^2}-2mt+\frac{1}{6}>{({b_n})_{max}}=\frac{1}{6}$,计算即得结论.
解答 解:∵a1=2,an-an-1-2n=0(n≥2,n∈N),
∴a2=6,a3=12,
当n≥2时,an-an-1=2n,an-1-an-2=2(n-1),
并项相加,得:an-a1=2[n+(n-1)+…+3+2],
∴${a_n}=2[n+(n-1)+…+3+2+1]=2\frac{n(n+1)}{2}=n(n+1)$,
又∵当n=1时,a1=1×(1+1)=2也满足上式,
∴数列{an}的通项公式为an=n(n+1),
∴${b_n}=\frac{1}{{{a_{n+1}}}}+\frac{1}{{{a_{n+2}}}}+\frac{1}{{{a_{n+3}}}}+…+\frac{1}{{{a_{2n}}}}=\frac{1}{(n+1)(n+2)}+\frac{1}{(n+2)(n+3)}+…+\frac{1}{2n(2n+1)}$
=$\frac{1}{n+1}-\frac{1}{n+2}+\frac{1}{n+2}-\frac{1}{n+3}+…+\frac{1}{2n}-\frac{1}{2n+1}$
=$\frac{1}{n+1}-\frac{1}{2n+1}=\frac{n}{{2{n^2}+3n+1}}=\frac{1}{{2n+\frac{1}{n}+3}}$,
令$f(x)=2x+\frac{1}{x}(x≥1)$,则$f'(x)=2-\frac{1}{x^2}$,
∵当x≥1时,f'(x)>0恒成立,
∴f(x)在x∈[1,+∞)上是增函数,
故当x=1时,f(x)min=f(1)=3,即当n=1时,${({b_n})_{max}}=\frac{1}{6}$,
要使对任意的正整数n,当m∈[-1,1]时,不等式${t^2}-2mt+\frac{1}{6}>{b_n}$恒成立,
则须使${t^2}-2mt+\frac{1}{6}>{({b_n})_{max}}=\frac{1}{6}$,即t2-2mt>0对?m∈[-1,1]恒成立,
∴$\left\{{\begin{array}{l}{{t^2}-2t>0}\\{{t^2}+2t>0}\end{array}}\right.$解得t>2或t<-2,
∴实数t的取值范围为(-∞,-2)∪(2,+∞),
故答案为:(-∞,-2)∪(2,+∞).
点评 本题考查数列的通项及前n项和,涉及利用导数研究函数的单调性,考查运算求解能力,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ①④⑤⑥ | B. | ②④⑤ | C. | ③④⑤⑥ | D. | ①⑤⑥ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{x}$•sinx+1=0 | B. | $\frac{1}{x}$•sinx-1=0 | C. | x•sinx+1=0 | D. | x•sinx-1=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{9}{16}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
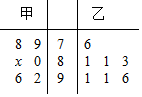 某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.
某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
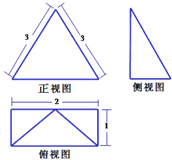 一个空间几何体的三视图如图,其中主视图是腰长为3的等腰三角形,俯视图是边长分别为1,2的矩形,则该几何体的体积等于( )
一个空间几何体的三视图如图,其中主视图是腰长为3的等腰三角形,俯视图是边长分别为1,2的矩形,则该几何体的体积等于( )| A. | 2 | B. | $4\sqrt{2}$ | C. | $\frac{{4\sqrt{3}}}{3}$ | D. | $\frac{{4\sqrt{2}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com