
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() 的长轴长为4.
的长轴长为4.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,是否存在实数
两点,是否存在实数![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1) ![]() ;(2) 存在实数
;(2) 存在实数![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ,理由见解析.
,理由见解析.
【解析】
(1)由长轴长为4,可得求出![]() ,再结合
,再结合![]() 及
及![]() ,即可求出
,即可求出![]() ,从而求出椭圆
,从而求出椭圆![]() 的方程;
的方程;
(2) 设![]() ,
,![]() ,将直线
,将直线![]() 的方程与椭圆
的方程与椭圆![]() 的方程联立消去
的方程联立消去![]() ,利用根与系数的关系求出
,利用根与系数的关系求出![]() ,
,![]() ,再由以线段
,再由以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ,可得
,可得![]() ,即
,即![]() ,将
,将![]() ,
,![]() 整体代入即可求出
整体代入即可求出![]() .
.
(1)因为椭圆![]() 的长轴长为4,所以
的长轴长为4,所以![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)存在实数![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() .
.
证明:设![]() ,
,![]() ,
,
由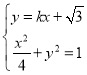 ,得
,得![]() ,
,
因为直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,
所以![]() ,所以
,所以![]() 或
或![]() ,
,
所以![]() ,
,![]() ,
,
所以![]()
因为以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() ,所以
,所以![]() ,
,
所以![]() ,即
,即![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以存在实数![]() 使得以线段
使得以线段![]() 为直径的圆恰好经过坐标原点
为直径的圆恰好经过坐标原点![]() .
.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2sin(ωx+φ)+1(![]() )的最小正周期为π,且
)的最小正周期为π,且![]() .
.
(1)求ω和φ的值;
(2)函数f(x)的图象纵坐标不变的情况下向右平移![]() 个单位,得到函数g(x)的图象,
个单位,得到函数g(x)的图象,
①求函数g(x)的单调增区间;
②求函数g(x)在![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,点
中,点![]() ,直线
,直线![]() ,设圆
,设圆![]() 的半径为1, 圆心在
的半径为1, 圆心在![]() 上.
上.

(1)若圆心![]() 也在直线
也在直线![]() 上,过点
上,过点![]() 作圆
作圆![]() 的切线,求切线方程;
的切线,求切线方程;
(2)若圆![]() 上存在点
上存在点![]() ,使
,使![]() ,求圆心
,求圆心![]() 的横坐标
的横坐标![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了引导居民合理用水,居民生活用水实行二级阶梯式水价计量方法,具体如下;第一阶梯,每户居民每月用水量不超过12吨,价格为4元/吨;第二阶梯,每户居民用水量超过12吨,超过部分的价格为8元/吨,为了了解全是居民月用水量的分布情况,通过抽样获得了100户居民的月用水量(单位:吨),将数据按照![]() (全市居民月用水量均不超过16吨)分成8组,制成了如图1所示的频率分布直方图.
(全市居民月用水量均不超过16吨)分成8组,制成了如图1所示的频率分布直方图.
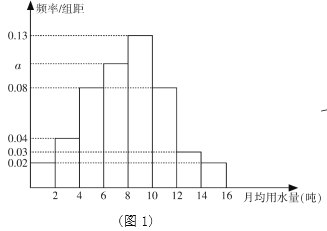
(Ⅰ)求频率分布直方图中字母![]() 的值,并求该组的频率;
的值,并求该组的频率;
(Ⅱ)通过频率分布直方图,估计该市居民每月的用水量的中位数![]() 的值(保留两位小数);
的值(保留两位小数);
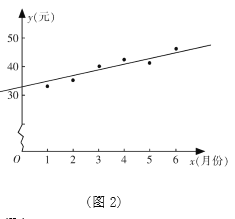
(Ⅲ)如图2是该市居民张某2016年1~6月份的月用水费![]() (元)与月份
(元)与月份![]() 的散点图,其拟合的线性回归方程是
的散点图,其拟合的线性回归方程是![]() 若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
若张某2016年1~7月份水费总支出为312元,试估计张某7月份的用水吨数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别是a,b,c,若sin A+cos A=1-sin![]() .
.
(1)求sin A的值;
(2)若c2-a2=2b,且sin B=3cos C,求b.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某景点为了了解游客人数的变化规律,提高旅游服务质量,收集并整理了2016年1月至2018年12月期间月接待游客量(单位:万人)的数据,绘制了下面的折线图:

根据该折线图,下列结论正确的是( )
A.各年1月至8月月接待游客量逐月增加
B.各年8月至12月月接待游客量逐月递减
C.各年的月接待游客量最低峰期在12月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设曲线y=xn+1(n∈N*)在点(1,1)处的切线与x轴的交点的横坐标为xn,令an=lgxn,则a1+a2+…+a99的值为( )
A. 1 B. 2 C. -2 D. -1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com