
【题目】已知椭圆![]() :
:![]() 的左焦点
的左焦点![]() ,点
,点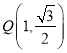 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)经过圆![]() :
:![]() 上一动点
上一动点![]() 作椭圆
作椭圆![]() 的两条切线,切点分别记为
的两条切线,切点分别记为![]() ,
,![]() ,直线
,直线![]() ,
,![]() 分别与圆
分别与圆![]() 相交于异于点
相交于异于点![]() 的
的![]() ,
,![]() 两点.
两点.
(i)当直线![]() ,
,![]() 的斜率都存在时,记直线
的斜率都存在时,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .求证:
.求证:![]() ;
;
(ii)求![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() ;(Ⅱ)(i)证明见解析;(ii)
;(Ⅱ)(i)证明见解析;(ii)![]() .
.
【解析】
(Ⅰ)把点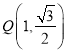 代入椭圆方程,结合
代入椭圆方程,结合![]() ,
,![]() ,即可求得椭圆的标准方程.
,即可求得椭圆的标准方程.
(Ⅱ)(i)设点![]() ,写出切线方程
,写出切线方程![]() ,联立方程组
,联立方程组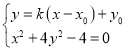 ,再由
,再由![]() ,结合韦达定理,写出
,结合韦达定理,写出![]() 的表达式,化简得出结果;
的表达式,化简得出结果;
(ii)设点![]() ,
,![]() ,进而求得直线
,进而求得直线![]() 和
和![]() 的直线方程,结合两条直线的形式,可写出直线
的直线方程,结合两条直线的形式,可写出直线![]() 的方程,运用弦长公式求得
的方程,运用弦长公式求得![]() ,结合
,结合![]() 的范围,可求得
的范围,可求得![]() 的取值范围.
的取值范围.
(Ⅰ)∵椭圆![]() 的左焦点
的左焦点![]() ,∴
,∴![]() .
.
将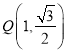 代入
代入![]() ,得
,得![]() .
.
又![]() ,∴
,∴![]() ,
,![]() .
.
∴椭圆![]() 的标准方程为
的标准方程为![]() .
.
(Ⅱ)(i)设点![]() ,设过点
,设过点![]() 与椭圆
与椭圆![]() 相切的直线方程为
相切的直线方程为![]() .
.
由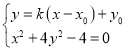 ,消去
,消去![]() ,得
,得![]() .
.
![]() .
.
令![]() ,整理得
,整理得![]() .
.
由已知,则![]() .
.
又![]() ,∴
,∴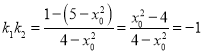 .
.
(ii)设点![]() ,
,![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 的方程为
的方程为![]() .
.
由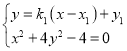 ,消去
,消去![]() ,得
,得![]() .
.
![]() .
.
令![]() ,整理得
,整理得![]() .
.
则![]() .
.
∴直线![]() 的方程为
的方程为![]() .
.
化简,可得![]() ,即
,即![]() .
.
经验证,当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为
的方程为![]() 或
或![]() ,也满足
,也满足![]() .
.
同理,可得直线![]() 的方程为
的方程为![]() .
.
∵![]() 在直线
在直线![]() ,
,![]() 上,∴
上,∴![]() ,
,![]() .
.
∴直线![]() 的方程为
的方程为![]() .
.
由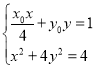 ,消去
,消去![]() ,得
,得![]() .
.
∴![]() ,
,![]() .
.
∴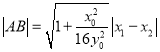
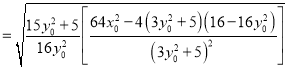
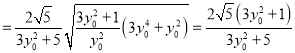 .
.
又由(i)可知当直线![]() ,
,![]() 的斜率都存在时,
的斜率都存在时,![]() ;易知当直线
;易知当直线![]() 或
或![]() 斜率不存在时,也有
斜率不存在时,也有![]() .
.
∴![]() 为圆
为圆![]() 的直径,即
的直径,即![]() .
.
∴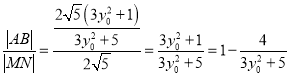 .
.
又![]() ,∴
,∴![]() .
.
∴![]() 的取值范围为
的取值范围为![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】我们打印用的A4纸的长与宽的比约为![]() ,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为
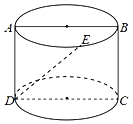
,之所以是这个比值,是因为把纸张对折,得到的新纸的长与宽之比仍约为![]() ,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
,纸张的形状不变.已知圆柱的母线长小于底面圆的直径长(如图所示),它的轴截面ABCD为一张A4纸,若点E为上底面圆上弧AB的中点,则异面直线DE与AB所成的角约为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的离心率为
的离心率为![]() ,且过点A(2,1).
,且过点A(2,1).
(1)求C的方程:
(2)点M,N在C上,且AM⊥AN,AD⊥MN,D为垂足.证明:存在定点Q,使得|DQ|为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司采购了一批零件,为了检测这批零件是否合格,从中随机抽测120个零件的长度(单位:分米),按数据分成![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 这6组,得到如图所示的频率分布直方图,其中长度大于或等于1.59分米的零件有20个,其长度分别为1.59,1.59,1.61,1.61,1.62,1.63,1.63,1.64,1.65,1.65,1.65,1.65,1.66,1.67,1.68,1.69,1.69,1.71,1.72,1.74,以这120个零件在各组的长度的频率估计整批零件在各组长度的概率.
这6组,得到如图所示的频率分布直方图,其中长度大于或等于1.59分米的零件有20个,其长度分别为1.59,1.59,1.61,1.61,1.62,1.63,1.63,1.64,1.65,1.65,1.65,1.65,1.66,1.67,1.68,1.69,1.69,1.71,1.72,1.74,以这120个零件在各组的长度的频率估计整批零件在各组长度的概率.
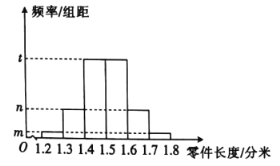
(1)求这批零件的长度大于1.60分米的频率,并求频率分布直方图中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)若从这批零件中随机选取3个,记![]() 为抽取的零件长度在
为抽取的零件长度在![]() 的个数,求
的个数,求![]() 的分布列和数学期望;
的分布列和数学期望;
(3)若变量![]() 满足
满足![]() 且
且![]() ,则称变量
,则称变量![]() 满足近似于正态分布
满足近似于正态分布![]() 的概率分布.如果这批零件的长度
的概率分布.如果这批零件的长度![]() (单位:分米)满足近似于正态分布
(单位:分米)满足近似于正态分布![]() 的概率分布,则认为这批零件是合格的将顺利被签收;否则,公司将拒绝签收.试问,该批零件能否被签收?
的概率分布,则认为这批零件是合格的将顺利被签收;否则,公司将拒绝签收.试问,该批零件能否被签收?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的左焦点
的左焦点![]() ,点
,点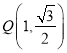 在椭圆
在椭圆![]() 上.
上.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)经过圆![]() :
:![]() 上一动点
上一动点![]() 作椭圆
作椭圆![]() 的两条切线,切点分别记为
的两条切线,切点分别记为![]() ,
,![]() ,直线
,直线![]() ,
,![]() 分别与圆
分别与圆![]() 相交于异于点
相交于异于点![]() 的
的![]() ,
,![]() 两点.
两点.
(i)求证:![]() ;
;
(ii)求![]() 的面积的取值范围.
的面积的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为梯形,
为梯形, ![]() ,且
,且![]() ,
, ![]() 是边长为2的正三角形,顶点
是边长为2的正三角形,顶点![]() 在
在![]() 上的射影为点
上的射影为点![]() ,且
,且![]() ,
, ![]() ,
, ![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com