
【题目】某公司生产的某种时令商品每件成本为![]() 元,经过市场调研发现,这种商品在未来
元,经过市场调研发现,这种商品在未来![]() 天内的日销售量
天内的日销售量![]() (件)与时间
(件)与时间![]() (天)的关系如下表所示.
(天)的关系如下表所示.
时间 | 1 | 3 | 6 | 10 | 36 | …… |
日销售量
| 94 | 90 | 84 | 76 | 24 | …… |
未来40天内,前20天每天的价格![]() (元/件)与时间
(元/件)与时间![]() (天)的函数关系式为
(天)的函数关系式为 ![]() ,且
,且![]() 为整数),后20天每天的价格
为整数),后20天每天的价格![]() (元/件)与时间
(元/件)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() ,且
,且![]() 为整数).
为整数).
(Ⅰ)认真分析表格中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据![]() (件)与
(件)与 ![]() (天)的关系式;
(天)的关系式;
(Ⅱ)试预测未来 40 天中哪一天的日销售利润最大,最大利润是多少?
(Ⅲ)在实际销售的前 20 天中,该公司决定每销售 1 件商品就捐赠![]() 元利润
元利润![]() 给希望工程. 公司通过销售记录发现,前 20 天中,每天扣除捐赠后的日销售利润随时间
给希望工程. 公司通过销售记录发现,前 20 天中,每天扣除捐赠后的日销售利润随时间![]() (天)的增大而增大,求
(天)的增大而增大,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)第14天时的销售利润最大,最大578元;(3)
;(2)第14天时的销售利润最大,最大578元;(3)![]() .
.
【解析】试题分析:(1)通过观察表格可知m与t是一次函数关系,设函数关系式为m=kt+b,代入计算即得结论;
(2)通过设日销售利润为W元,分1≤t≤20、21≤t≤40两种情况讨论,利用“销售利润=销售收入-成本”分别计算出前20天、后20天中的最大日获利润,比较即得结论;
(3)通过写出扣除捐赠后每天的日销售利润![]() ,结合W随t的增大而增大可知函数W的图象的对称轴t=14+2a>19.5,进而计算可得结论.
,结合W随t的增大而增大可知函数W的图象的对称轴t=14+2a>19.5,进而计算可得结论.
试题解析:
(1)![]() .
.
(2)设日销售利润为![]() 元,当
元,当![]() 时,
时,
![]()
所以当![]() 时,
时, ![]() 有最大值578元。
有最大值578元。
当![]() 时,
时, ![]()
因当![]() 时,
时, ![]() 随
随![]() 增大而减小,故当
增大而减小,故当![]() 时,
时, ![]() 有最大值513
有最大值513
综上所述,第14天时的销售利润最大,最大578元.
(3)![]()
对称轴为![]() ,
,
![]() ,且
,且![]() 为整数,
为整数, ![]() 随
随![]() 的增大而增大,
的增大而增大,
![]()
![]() ,故
,故![]()


科目:高中数学 来源: 题型:
【题目】某企业接到生产3000台某产品的A,B,C三种部件的订单,每台产品需要这三种部件的数量分别为2,2,1(单位:件).已知每个工人每天可生产A部件6件,或B部件3件,或C部件2件.该企业计划安排200名工人分成三组分别生产这三种部件,生产B部件的人数与生产A部件的人数成正比,比例系数为k(k为正整数).
(1)设生产A部件的人数为x,分别写出完成A,B,C三种部件生产需要的时间;
(2)假设这三种部件的生产同时开工,试确定正整数k的值,使完成订单任务的时间最短,并给出时间最短时具体的人数分组方案.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长均相等的正三棱柱ABCA1B1C1中,D为BB1的中点,F在AC1上,且DF⊥AC1,则下述结论:
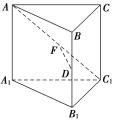
①AC1⊥BC;
②AF=FC1;
③平面DAC1⊥平面ACC1A1,其中正确的个数为( )
A.0 B.1
C.2 D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
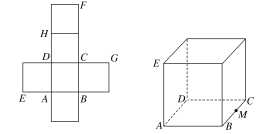
【题目】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={x|2-a≤x≤2+a},B={x|x≤1或x≥4}.
(1)当a=3时,求A∩B;
(2)若a>0,且A∩B=![]() ,求实数a的取值范围.
,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某市的高一学生中随机抽取400名同学的体重进行统计,得到如图所示频率分布直方图.
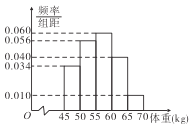
(Ⅰ)估计从该市高一学生中随机抽取一人,体重超过![]() 的概率;
的概率;
(Ⅱ)假设该市高一学生的体重![]() 服从正态分布
服从正态分布![]() .
.
(ⅰ)利用(Ⅰ)的结论估计该高一某个学生体重介于![]() 之间的概率;
之间的概率;
(ⅱ)从该市高一学生中随机抽取3人,记体重介于![]() 之间的人数为
之间的人数为![]() ,利用(ⅰ)的结论,求
,利用(ⅰ)的结论,求![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com