
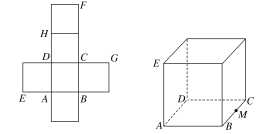
【题目】一个正方体的平面展开图及该正方体直观图的示意图如图所示,在正方体中,设BC的中点为M,GH的中点为N。
(1)请将字母F,G,H标记在正方体相应的顶点处(不需说明理由);
(2)证明:直线MN∥平面BDH;
(3)过点M,N,H的平面将正方体分割为两部分,求这两部分的体积比.
科目:高中数学 来源: 题型:
【题目】东亚运动会将于2013年10月6日在天津举行.为了搞好接待工作,组委会打算学习北京奥运会招募大量志愿者的经验,在某学院招募了16名男志愿者和14名女志愿者,调查发现,男女志愿者中分别有10人和6人喜爱运动,其余人不喜欢运动.
(1)根据以上数据完成以下2×2列联表:
喜爱运动 | 不喜爱运动 | 总计 | |
男 | 10 | 16 | |
女 | 6 | 14 | |
总计 | 30 |
(2)根据列联表的独立性检验,能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关?
(3)如果从喜欢运动的女志愿者中(其中恰有4人会外语),抽取2名负责翻译工作,那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少?
参考公式:K2=![]() ,其中
,其中
n=a+b+c+d.
参考数据:
P(K2≥k) | 0.40 | 0.25 | 0.10 | 0.010 |
k | 0.708 | 1.323 | 2.706 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解人们对于国家新颁布的“生育二胎放开”政策的热度,现在某市进行调查,随机抽调了50人,他们年龄的频数分布及支持“生育二胎”人数如下表:

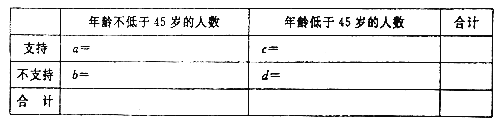
(1)由以上统计数据填下面![]() 列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
列联表,并问是否有99%的把握认为以45岁为分界点对“生育二胎放开”政策的支持度有差异;
(2)若对年龄在![]() 的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?
的被调查人中各随机选取两人进行调查,恰好这两人都支持“生育二胎放开”的概率是多少?

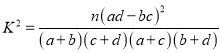
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,六面体ABCDHEFG中,四边形ABCD为菱形,AE,BF,CG,DH都垂直于平面ABCD.若DA=DH=DB=4,AE=CG=3。
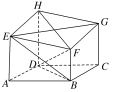
(1)求证:EG⊥DF;
(2)求BE与平面EFGH所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,给出下列结论:
,给出下列结论:
(1)若对任意![]() ,且
,且![]() ,都有
,都有![]() ,则
,则![]() 为R上的减函数;
为R上的减函数;
(2)若![]() 为R上的偶函数,且在
为R上的偶函数,且在![]() 内是减函数,
内是减函数, ![]() (-2)=0,则
(-2)=0,则![]() >0解集为(-2,2);
>0解集为(-2,2);
(3)若![]() 为R上的奇函数,则
为R上的奇函数,则![]() 也是R上的奇函数;
也是R上的奇函数;
(4)t为常数,若对任意的![]() ,都有
,都有![]() 则
则![]() 关于
关于![]() 对称。
对称。
其中所有正确的结论序号为_________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产的某种时令商品每件成本为![]() 元,经过市场调研发现,这种商品在未来
元,经过市场调研发现,这种商品在未来![]() 天内的日销售量
天内的日销售量![]() (件)与时间
(件)与时间![]() (天)的关系如下表所示.
(天)的关系如下表所示.
时间 | 1 | 3 | 6 | 10 | 36 | …… |
日销售量
| 94 | 90 | 84 | 76 | 24 | …… |
未来40天内,前20天每天的价格![]() (元/件)与时间
(元/件)与时间![]() (天)的函数关系式为
(天)的函数关系式为 ![]() ,且
,且![]() 为整数),后20天每天的价格
为整数),后20天每天的价格![]() (元/件)与时间
(元/件)与时间![]() (天)的函数关系式为
(天)的函数关系式为![]() ,且
,且![]() 为整数).
为整数).
(Ⅰ)认真分析表格中的数据,用所学过的一次函数、二次函数、反比例函数的知识确定一个满足这些数据![]() (件)与
(件)与 ![]() (天)的关系式;
(天)的关系式;
(Ⅱ)试预测未来 40 天中哪一天的日销售利润最大,最大利润是多少?
(Ⅲ)在实际销售的前 20 天中,该公司决定每销售 1 件商品就捐赠![]() 元利润
元利润![]() 给希望工程. 公司通过销售记录发现,前 20 天中,每天扣除捐赠后的日销售利润随时间
给希望工程. 公司通过销售记录发现,前 20 天中,每天扣除捐赠后的日销售利润随时间![]() (天)的增大而增大,求
(天)的增大而增大,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
已知直线![]() 的参数方程为
的参数方程为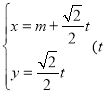 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .且曲线
.且曲线![]() 的左焦点
的左焦点![]() 在直线
在直线![]() 上.
上.
(1)若直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,求
两点,求![]() 的值;
的值;
(2)求曲线![]() 的内接矩形的周长的最大值.
的内接矩形的周长的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点P(2,2),圆C:x2+y2-8y=0,过点P的动直线l与圆C交于A,B两点,线段AB的中点为M,O为坐标原点.
(1)求M的轨迹方程;
(2)当|OP|=|OM|时,求l的方程及△POM的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com