
分析 (1)根据题意画出图形,结合图形,表示出PA•PB,求出它取最小值时直线l的方程即可.
(2)因为△AOB的面积为S,设直线l的斜率为k(k<0),则过点P(-1,-2)的直线l的直线方程为y+2=k(x+1),根据三角形的面积公式得到2S=|k-2|•|$\frac{2}{k}$-1|,即为k2+(2S-4)k+4=0,根据判别式讨论解得情况,即可得到直线l的条数.
解答 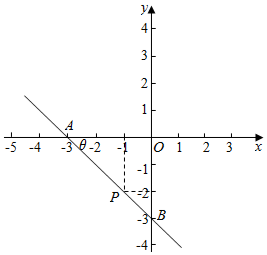 解:(1)根据题意,画出图形,如图所示:
解:(1)根据题意,画出图形,如图所示:
设∠BAO=θ,则0°<θ<90°,
PA=$\frac{2}{sinθ}$,PB=$\frac{1}{cosθ}$,
∴PA•PB=$\frac{2}{sinθ}$•$\frac{1}{cosθ}$=$\frac{4}{sin2θ}$,
当2θ=90°,即θ=45°时,
PA•PB取得最小值,
此时直线的倾斜角为135°,斜率为-1,
∴直线l的方程为y+2=-1(x+1),
化简得x+y+3=0,
(2)因为△AOB的面积为S,设直线l的斜率为k(k<0),
∴点P(-1,-2)的直线l的直线方程为y+2=k(x+1),
当x=0时,y=k-2,
当y=0时,x=$\frac{2}{k}$-1,
∴2S=|k-2|•|$\frac{2}{k}$-1|=(2-k)(1-$\frac{2}{k}$)=2+2-$\frac{4}{k}$-k,
∴k2+(2S-4)k+4=0,
当△<0时,即(2S-4)2-4×4<0,解得0<S<4时,方程无解,此时直线的条数为0,
当△=0时,即(2S-4)2-4×4=0,解得S=4时,方程有一个解,解得k=-2,此时直线的条数为1,
当△>0时,即(2S-4)2-4×4>0,解得S>4时,方程有两个解,解得k=-(s-2)±$\sqrt{(s-2)^{2}-4}$<0,此时直线的条数为2.
点评 本题考查直角三角形中的边角关系,三角函数的最值问题,也考查了用点斜式求直线的方程的应用问题,以及根的判别式的应用,属于中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | 1 | D. | $\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 空间三点确定一个平面 | |
| B. | 过直线外一点有且只有一条直线与已知直线垂直 | |
| C. | 如果一条直线与平面内的一条直线平行,则这条直线与平面平行 | |
| D. | 三个平面最多将可空间分成八块 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | $\frac{9}{2}$ | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
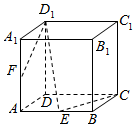 如图所示,在正方体AC1中,E,F分别是AB,AA1的中点.
如图所示,在正方体AC1中,E,F分别是AB,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com