
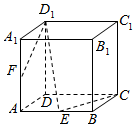
 如图所示,在正方体AC1中,E,F分别是AB,AA1的中点.
如图所示,在正方体AC1中,E,F分别是AB,AA1的中点.分析 (1)证明EC与D1F相交,设交点为P,再证明P在平面ABCD与平面ABCD的交线上,即可证明CE、D1F、DA三线共点;
(2)证明P,E,H都在平面PCD1与平面ABCD的交线上,即可得出P,E,H三点共线.
解答 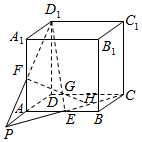 解:(1)证明:正方体AC1中,E,F分别是AB,AA1的中点,
解:(1)证明:正方体AC1中,E,F分别是AB,AA1的中点,
∴EF∥CD1且EF≠CD1,∴EC与D1F相交,设交点为P,
∵P∈EC,EC⊆平面ABCD,∴P∈平面ABCD;
又∵P∈FD1,FD1⊆平面ADD1A1,∴P∈平面ADD1A1,
∴P为两平面的公共点,
平面ABCD∩平面ADD1A1=AD,∴P∈AD,
∴CE、D1F、DA三线共点于P;
(2)证明:如图所示,
在(1)的结论中,G是D1E上一点,FG交平面ABCD于点H,
则FH?平面PCD1,∴H∈平面PCD1,又H∈平面ABCD,
∴H∈平面PCD1∩平面ABCD,
同理,P∈平面PCD1∩平面ABCD,
E∈平面PCD1∩平面ABCD,
∴P,E,H都在平面PCD1与平面ABCD的交线上,
∴P,E,H三点共线.
点评 本题考查了立体几何中的点线面的位置关系与应用问题,也考查了数形结合与逻辑推理能力,是综合性题目.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{a}$⊥$\overrightarrow{b}$ | B. | $\overrightarrow{a}$∥$\overrightarrow{b}$ | C. | $\overrightarrow{a}$⊥($\overrightarrow{a}$+$\overrightarrow{b}$) | D. | $\overrightarrow{a}$⊥($\overrightarrow{a}$-$\overrightarrow{b}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com