
分析 化简可得$\frac{1}{{a}_{n+1}}$=$\frac{{2}^{n+1}+{a}_{n}}{{2}^{n+1}{a}_{n}}$=$\frac{1}{{a}_{n}}$+$\frac{1}{{2}^{n+1}}$,从而可得$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=$\frac{1}{{2}^{n}}$,从而利用累加法求和即可.
解答 解:∵an+1=$\frac{{2}^{n+1}•{a}_{n}}{{2}^{n+1}+{a}_{n}}$,
∴$\frac{1}{{a}_{n+1}}$=$\frac{{2}^{n+1}+{a}_{n}}{{2}^{n+1}{a}_{n}}$=$\frac{1}{{a}_{n}}$+$\frac{1}{{2}^{n+1}}$,
∴$\frac{1}{{a}_{n+1}}$-$\frac{1}{{a}_{n}}$=$\frac{1}{{2}^{n+1}}$,
∴$\frac{1}{{a}_{2}}$-$\frac{1}{{a}_{1}}$=$\frac{1}{{2}^{2}}$,
$\frac{1}{{a}_{3}}$-$\frac{1}{{a}_{2}}$=$\frac{1}{{2}^{3}}$,
…
$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{n-1}}$=$\frac{1}{{2}^{n}}$,
利用累加法可得,
$\frac{1}{{a}_{n}}$-$\frac{1}{{a}_{1}}$=$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$,
又∵a1=2,∴$\frac{1}{{a}_{1}}$=$\frac{1}{2}$;
∴$\frac{1}{{a}_{n}}$=$\frac{1}{2}$+$\frac{1}{{2}^{2}}$+$\frac{1}{{2}^{3}}$+…+$\frac{1}{{2}^{n}}$=$\frac{\frac{1}{2}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}$=1-$\frac{1}{{2}^{n}}$,
∴an=$\frac{1}{1-\frac{1}{{2}^{n}}}$=$\frac{{2}^{n}}{{2}^{n}-1}$.
点评 本题考查了数列的性质的判断及转化思想的应用,同时考查了整体思想与构造法的应用.


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:高中数学 来源: 题型:解答题
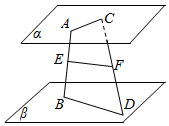 已知:如图,平面α、β满足α∥β,A、C∈α,B、D∈β,E∈AB,F∈CD,AC与BD异面,且$\frac{AE}{EB}=\frac{CF}{FD}$.求证:EF∥β
已知:如图,平面α、β满足α∥β,A、C∈α,B、D∈β,E∈AB,F∈CD,AC与BD异面,且$\frac{AE}{EB}=\frac{CF}{FD}$.求证:EF∥β查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
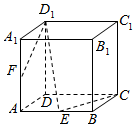 如图所示,在正方体AC1中,E,F分别是AB,AA1的中点.
如图所示,在正方体AC1中,E,F分别是AB,AA1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com