
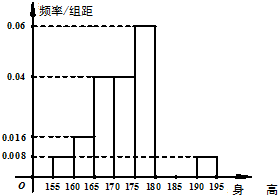
 从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.
从某学校的800名男生中随机抽取50名测量身高,被测学生身高全部介于155cm和195cm之间,将测量结果按如下方式分成八组:第一组[155,160),第二组[160,165),…,第八组[190,195],如图是按上述分组方法得到的频率分布直方图的一部分,已知第一组与第八组人数相同,第六组的人数为4人.| 4 |
| 50 |
| 7 |
| 15 |


科目:高中数学 来源: 题型:
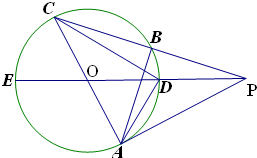 如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD.
如图,PA是⊙O的切线,PE过圆心0,AC为⊙O的直径,PC与⊙O相交于B、C两点,连接AB、CD.| PA2 |
| PC•PE |
| BD |
| AD |
查看答案和解析>>
科目:高中数学 来源: 题型:
8
| ||
| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 在线路中,各原件能否正常工作是相互独立的,已知原件a,b,c,d,e能正常工作的概率是0.9,0.95,0.7,0.8,0.85,求线路畅通的概率.
在线路中,各原件能否正常工作是相互独立的,已知原件a,b,c,d,e能正常工作的概率是0.9,0.95,0.7,0.8,0.85,求线路畅通的概率.查看答案和解析>>
科目:高中数学 来源: 题型:
| 兴趣小组 | 小组人数 | 抽取人数 |
| A | 24 | x |
| B | 36 | 3 |
| C | 48 | y |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com