
【题目】在四棱锥P-ABCD中,PA![]() 平面ABCD,菱形ABCD的边长为2,且
平面ABCD,菱形ABCD的边长为2,且![]() ,点E、F分别是PA,CD的中点,
,点E、F分别是PA,CD的中点,
(1)求证:EF![]() 平面PBC
平面PBC
(2)若PC与平面ABCD所成角的大小为![]() ,求C到平面PBD的距离
,求C到平面PBD的距离
【答案】(1)证明见详解;(2)![]()
【解析】
(1)取![]() 的中点
的中点![]() ,连接
,连接![]() ,由三角形中位线的性质可证
,由三角形中位线的性质可证![]() ,即可证明平面
,即可证明平面![]() 平面
平面![]() ,从而得证结论.
,从而得证结论.
(2)将点到面的距离问题转化为求三棱锥的高的问题,利用等体积法即可得到答案.
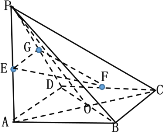
(1)如图取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为点E、F分别是PA,CD的中点,
所以![]() 分别为
分别为![]() 和
和![]() 中位线,
中位线,
所以![]() ,
,
又![]() ,
,
所以平面![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
(2)连接![]() 交于点
交于点![]() ,连接
,连接![]() .
.
设点![]() 到平面
到平面![]() 的距离为
的距离为![]()
因为菱形ABCD的边长为2,且![]() ,
,
所以![]() ,且
,且![]() 为等边三角形,
为等边三角形,
所以![]() ,且
,且![]() ,
,
因为![]() 平面
平面![]()
所以![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角,
所成的角,
所以![]() ,所以
,所以![]() ,
,
又四边形![]() 为菱形,所以
为菱形,所以![]() ,
,
所以![]() ,所以
,所以![]()
又![]() ,
,
所以![]() 的面积为
的面积为![]()
所以![]()
依题![]() 为三棱锥
为三棱锥![]() 的高,
的高,
且![]() 的面积为
的面积为![]() ,
,
所以三棱锥![]() 的体积为
的体积为
![]() ,
,
又因为![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:
【题目】手机运动计步已经成为一种新时尚.某单位统计了职工一天行走步数(单位:百步),绘制出如下频率分布直方图:
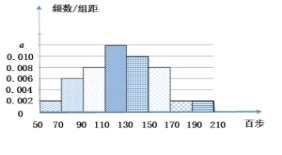
(1)求直方图中a的值,并由频率分布直方图估计该单位职工一天步行数的中位数;
(2)若该单位有职工200人,试估计职工一天行走步数不大于13000的人数;
(3)在(2)的条件下,该单位从行走步数大于15000的3组职工中用分层抽样的方法选取6人参加远足拉练活动,再从6人中选取2人担任领队,求这两人均来自区间![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市有一家大型共享汽车公司,在市场上分别投放了黄、蓝两种颜色的汽车,已知黄、蓝两种颜色的汽车的投放比例为![]() .监管部门为了了解这两种颜色汽车的质量,决定从投放到市场上的汽车中随机抽取5辆汽车进行试驾体验,假设每辆汽车被抽取的时能性相同.
.监管部门为了了解这两种颜色汽车的质量,决定从投放到市场上的汽车中随机抽取5辆汽车进行试驾体验,假设每辆汽车被抽取的时能性相同.
(1)求抽取的5辆汽车中恰有2辆是蓝色汽车的概率;
(2)在试驾体验过程中,发现蓝色汽车存在一定质量问题,监管部门决定从投放的汽车中随机地抽取一辆送技术部门作进一步抽样检测,并规定:若抽取的是黄色汽车.则将其放回市场,并继续随机地抽取下一辆汽车;若抽到的是蓝色汽车,则抽样结束;并规定抽样的次数不超过![]() 次,在抽样结束时,若已取到的黄色汽车数以
次,在抽样结束时,若已取到的黄色汽车数以![]() 表示,求
表示,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若椭圆![]() 的离心率等于
的离心率等于![]() ,抛物线
,抛物线![]() 的焦点在椭圆
的焦点在椭圆![]() 的顶点上.
的顶点上.
(1)求抛物线![]() 的方程;
的方程;
(2)若过![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 、
、![]() 两点,又过
两点,又过![]() 、
、![]() 作抛物线
作抛物线![]() 的切线
的切线![]() 、
、![]() ,当
,当![]() 时,求直线
时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列关于命题的说法错误的是( )
A.命题“若x2﹣3x+2=0,则x=2”的逆否命题为“若x≠2,则x2﹣3x+2≠0”
B.“a=2”是“函数f(x)=ax在区间(﹣∞,+∞)上为增函数”的充分不必要条件
C.命题“x∈R,使得x2+x+1<0”的否定是:“x∈R,均有x2+x+1≥0”
D.“若f ′(![]() )=0,则
)=0,则![]() 为y=f(x)的极值点”为真命题
为y=f(x)的极值点”为真命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,以原点为圆心,椭圆
,以原点为圆心,椭圆![]() 的短半轴长为半径的圆与直线
的短半轴长为半径的圆与直线![]() 相切.
相切.
(Ⅰ)求椭圆方程;
(Ⅱ)设![]() 为椭圆右顶点,过椭圆
为椭圆右顶点,过椭圆![]() 的右焦点的直线
的右焦点的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点(异于
两点(异于![]() ),直线
),直线![]() ,
,![]() 分别交直线
分别交直线![]() 于
于![]() ,
,![]() 两点. 求证:
两点. 求证:![]() ,
,![]() 两点的纵坐标之积为定值.
两点的纵坐标之积为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C所对的边分别为a,b,c,且acosC+ccosA=2bcosA.
(1)求角A的值;
(2)若![]() ,
, ![]() ,求△ABC的面积S.
,求△ABC的面积S.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,是一个半圆柱与多面体![]() 构成的几何体,平面
构成的几何体,平面![]() 与半圆柱的下底面共面,且
与半圆柱的下底面共面,且![]() ,
, ![]() 为弧
为弧![]() 上(不与
上(不与![]() 重合)的动点.
重合)的动点.
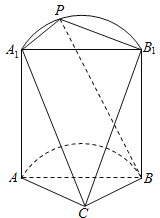
(1)证明: ![]() 平面
平面![]() ;
;
(2)若四边形![]() 为正方形,且
为正方形,且![]() ,
, ![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com