
【题目】已知等轴双曲线![]() :
:![]() 的右焦点为
的右焦点为![]() ,
,![]() 为坐标原点,过
为坐标原点,过![]() 作一条渐近线的垂线
作一条渐近线的垂线![]() 且垂足为
且垂足为![]() ,
,![]() .
.
(1)求等轴双曲线![]() 的方程;
的方程;
(2)若过点![]() 且方向向量为
且方向向量为![]() 的直线
的直线![]() 交双曲线
交双曲线![]() 于
于![]() 、
、![]() 两点,求
两点,求![]() 的值;
的值;
(3)假设过点![]() 的动直线
的动直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,试问:在
两点,试问:在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使得
,使得![]() 为常数,若存在,求出
为常数,若存在,求出![]() 的坐标,若不存在,试说明理由.
的坐标,若不存在,试说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)定点
;(3)定点![]() .
.
【解析】
(1)根据双曲线焦点到渐近线的距离为![]() 和等轴双曲线的性质,求得等轴双曲线
和等轴双曲线的性质,求得等轴双曲线![]() 的方程.
的方程.
(2)由直线![]() 的方向向量求得直线
的方向向量求得直线![]() 的斜率,由此写出直线
的斜率,由此写出直线![]() 的方程.联立直线
的方程.联立直线![]() 的方程和双曲线的方程,写出韦达定理,求得
的方程和双曲线的方程,写出韦达定理,求得![]() ,
,![]() ,由此求得
,由此求得![]() 的值.
的值.
(3)设![]() ,设出直线
,设出直线![]() 的方程,与双曲线方程联立,写出韦达定理,代入
的方程,与双曲线方程联立,写出韦达定理,代入![]() 进行化简,结合
进行化简,结合![]() 为常数列方程,解方程求得
为常数列方程,解方程求得![]() 点的坐标.
点的坐标.
(1)双曲线焦点到渐近线的距离为![]() ,所以
,所以![]() ,所以等轴双曲线
,所以等轴双曲线![]() 的方程为
的方程为![]() .且
.且![]() .
.
(2)由于直线![]() 的方向行向量为
的方向行向量为![]() ,所以直线
,所以直线![]() 的斜率为
的斜率为![]() ,而
,而![]() ,所以
,所以![]() :
:![]() ,与
,与![]() 联立方程并化简得
联立方程并化简得![]() ,可得
,可得![]() ,
,![]() ,
,
即![]() .
.
(3)设![]() 点
点![]() .依题意可知直线
.依题意可知直线![]() 与
与![]() 不平行,设直线
不平行,设直线![]() ,与
,与![]() 联立方程有
联立方程有![]() ,
,
可得![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
![]() ,要为定值,
,要为定值,
需满足![]() ,∴
,∴![]() ,即定点
,即定点![]() .
.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:
【题目】设关于![]() 的一元二次方程
的一元二次方程![]() .
.
(1)若![]() 是从0,1,2,3,4五个数中任取的一个数,
是从0,1,2,3,4五个数中任取的一个数,![]() 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数,![]() 是从区间
是从区间![]() 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙、丙三位同学在某次考试中总成绩列前三名,有![]() ,
,![]() ,
,![]() 三位学生对其排名猜测如下:
三位学生对其排名猜测如下:![]() :甲第一名,乙第二名;
:甲第一名,乙第二名;![]() :丙第一名;甲第二名;
:丙第一名;甲第二名;![]() :乙第一名,甲第三名.成绩公布后得知,
:乙第一名,甲第三名.成绩公布后得知,![]() ,
,![]() ,
,![]() 三人都恰好猜对了一半,则第一名是__________.
三人都恰好猜对了一半,则第一名是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为抛物线![]()
![]() 的焦点,过F且倾斜角为
的焦点,过F且倾斜角为![]() 的直线交抛物线于A,B两点,
的直线交抛物线于A,B两点,![]() .
.
(1)求抛物线的方程:
(2)已知![]() 为抛物线上一点,M,N为抛物线上异于P的两点,且满足
为抛物线上一点,M,N为抛物线上异于P的两点,且满足![]() ,试探究直线MN是否过一定点?若是,求出此定点;若不是,说明理由.
,试探究直线MN是否过一定点?若是,求出此定点;若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半圆![]() :
:![]() ,
,![]() 、
、![]() 分别为半圆
分别为半圆![]() 与
与![]() 轴的左、右交点,直线
轴的左、右交点,直线![]() 过点
过点![]() 且与
且与![]() 轴垂直,点
轴垂直,点![]() 在直线
在直线![]() 上,纵坐标为
上,纵坐标为![]() ,若在半圆
,若在半圆![]() 上存在点
上存在点![]() 使
使![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]()
![]() 的离心率为
的离心率为![]() ,椭圆短轴的一个端点与两个焦点构成的三角形的面积为
,椭圆短轴的一个端点与两个焦点构成的三角形的面积为![]() ,直线l的方程为:
,直线l的方程为:![]()
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)已知直线l与椭圆![]() 相交于
相交于![]() 、
、![]() 两点
两点
①若线段![]() 中点的横坐标为
中点的横坐标为![]() ,求斜率
,求斜率![]() 的值;
的值;
②已知点![]() ,求证:
,求证:![]() 为定值
为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分12分)袋中装有黑色球和白色球共7个,从中任取2个球都是白色球的概率为![]() .现有甲、乙两人从袋中轮流摸出1个球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后终止.每个球在每一次被摸出的机会都是等可能的,用X表示摸球终止时所需摸球的次数.
.现有甲、乙两人从袋中轮流摸出1个球,甲先摸,乙后摸,然后甲再摸,……,摸后均不放回,直到有一人摸到白色球后终止.每个球在每一次被摸出的机会都是等可能的,用X表示摸球终止时所需摸球的次数.
(1)求随机变量X的分布列和均值E(X);
(2)求甲摸到白色球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知U=R且A={x|a2x2-5ax-6<0},B{x||x-2|≥1}.
(1)若a=1,求(UA)![]() B;
B;
(2)求不等式a2x2-5ax-6<0(a∈R)的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年7月18日15时,超强台风“威马逊”登陆海南省.据统计,本次台风造成全省直接经济损失119.52亿元,适逢暑假,小明调查住在自己小区的50户居民由于台风造成的经济损失,作出如下频率分布直方图:
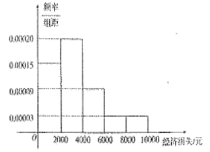
| 经济损失4000元以下 | 经济损失4000元以上 | 合计 |
捐款超过500元 | 30 | ||
捐款低于500元 | 6 | ||
合计 |
(1)台风后区委会号召小区居民为台风重灾区捐款,小明调查的50户居民捐款情况如上表,在表格空白处填写正确数字,并说明是否有![]() 以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
以上的把握认为捐款数额是否多于或少于500元和自身经济损失是否到4000元有关?
(2)台风造成了小区多户居民门窗损坏,若小区所有居民的门窗均由李师傅和张师傅两人进行维修,李师傅每天早上在7:00到8:00之间的任意时刻来到小区,张师傅每天早上在7:30到8:30分之间的任意时刻来到小区,求连续3天内,李师傅比张师傅早到小区的天数的分布列和数学期望.
附:临界值表
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
参考公式:![]() ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com