
分析 (1)连接ON、OM,则△ONM为直角三角形,利用||MN|=|MP|,求M点的轨迹方程;表示出|MN|,利用配方法求|MN|的最小值;
(2)以M为圆心的圆与圆O有公共点,半径最小时为与圆O相切的情形,而这些半径的最小值为圆O到直线l的距离减去圆O的半径,即可求出半径最小的圆的方程.
解答 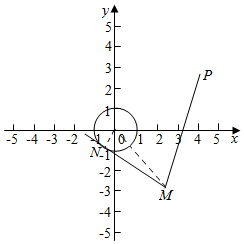 解 (1)连接ON、OM,则△ONM为直角三角形,
解 (1)连接ON、OM,则△ONM为直角三角形,
又||MN|=|MP|
所以|OM|2=|ON|2+|MN|2=1+|MP|2,
所以a2+b2=1+(a-4)2+(b-3)2,故M的轨迹方程是4x+3y-13=0.
由|MN|2=|OM|2-1=a2+b2-1=a2+(-$\frac{4}{3}$a+$\frac{13}{3}$)2-1=5a2-12a+8=$\frac{25}{9}$(a-$\frac{52}{25}$)2+$\frac{169}{25}$,
得|MN|min=$\frac{13}{5}$.
(3)以M为圆心的圆与圆O有公共点,半径最小时为与圆O相切的情形,而这些半径的最小值为圆O到直线l的距离减去圆O的半径,圆心M为过原点且与l垂直的直线l′与l的交点P0,所以r=$\frac{13}{5}$-1=$\frac{8}{5}$,
又l′:3x-4y=0,联立l:4x+3y-13=0得P0($\frac{52}{25}$,$\frac{39}{25}$).
所以所求圆的方程为(x-$\frac{52}{25}$)2+(y-$\frac{39}{25}$)2=($\frac{8}{5}$)2.
点评 本题考查轨迹方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-3} | B. | {2,-3} | C. | {-3,$\frac{1}{2}$} | D. | {-3,2,$\frac{1}{2}$} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com