
| 月份 | 用气量 | 煤气费 |
| 一月份 | 4m3 | 4元 |
| 二月份 | 25m3 | 14元 |
| 三月份 | 35m3 | 19元 |
| A. | 11.5元 | B. | 11元 | C. | 10.5元 | D. | 10元 |
分析 根据待定系数法求出A、B、C的值,求出f(x)的表达式,从而求出f(20)的值即可.
解答 解:由题意得:C=4,
将(25,14),(35,19)代入f(x)=4+B(x-A),得:
$\left\{\begin{array}{l}{4+B(25-A)=14}\\{4+B(35-A)=19}\end{array}\right.$,解得$\left\{\begin{array}{l}{A=5}\\{B=\frac{1}{2}}\end{array}\right.$,
∴f(x)=$\left\{\begin{array}{l}{4,0<x≤5}\\{4+\frac{1}{2}(x-5),x>5}\end{array}\right.$,
故x=20时:f(20)=11.5,
故选:A.
点评 本题考查了求函数的解析式问题,考查函数求值问题,是一道中档题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:填空题
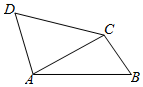 如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.
如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{2}$,+∞) | B. | (2,+∞) | C. | (-∞,2) | D. | (-∞,-$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+ln2}{2}$ | B. | $\frac{1+2ln2}{4}$ | C. | $\frac{1-ln2}{2}$ | D. | $\frac{3-2ln2}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|1<x<2} | B. | {x|1≤x≤2} | C. | {x|1≤x<2} | D. | {x|0≤x≤2} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com