
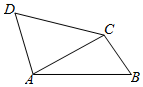
 如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.
如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$. 分析 在△BAC中,由余弦定理可得:AC2=42+22-2×4×2×cos60°,AC=2$\sqrt{3}$.在△ADC中,设∠CAD=α,则∠ACD=120°-α.由于△ADC是锐角三角形,可得30°<α<90°.
由正弦定理可得:$\frac{AD}{sin(12{0}^{°}-α)}$=$\frac{DC}{sinα}$=$\frac{2\sqrt{3}}{sin6{0}^{°}}$=4.化简整理即可得出.
解答 解:在△BAC中,由余弦定理可得:AC2=42+22-2×4×2×cos60°=12.
∴AC=2$\sqrt{3}$.
在△ADC中,设∠CAD=α,则∠ACD=120°-α.
∵△ADC是锐角三角形,∴0°<α<90°,0°<120°-α<90°,可得30°<α<90°.
由正弦定理可得:$\frac{AD}{sin(12{0}^{°}-α)}$=$\frac{DC}{sinα}$=$\frac{2\sqrt{3}}{sin6{0}^{°}}$=4.
∴AD=4sin(120°-α),DC=4sinα,
∴AD+DC=4sin(120°-α)+4sinα=$4(\frac{\sqrt{3}}{2}cosα+\frac{1}{2}sinα+sinα)$
=$4\sqrt{3}$$(\frac{\sqrt{3}}{2}sinα+\frac{1}{2}cosα)$
=4$\sqrt{3}$sin(α+30°),
∵30°<α<90°,∴60°<α+30°<120°,
∴sin(α+30°)∈$(\frac{\sqrt{3}}{2},1]$.
∴AD+DC∈$(6,4\sqrt{3}]$.
故答案为:$(6,4\sqrt{3}]$.
点评 本题考查了正弦定理弦定理、和差化积、三角函数的单调性,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{e-1}{2}$,1)∪(1,e-1) | B. | ($\frac{e-1}{2}$,1)∪(1,e-1] | C. | ($\frac{e-1}{3}$,1)∪(1,e-1) | D. | ($\frac{e-1}{3}$,1)∪(1,e-1] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 月份 | 用气量 | 煤气费 |
| 一月份 | 4m3 | 4元 |
| 二月份 | 25m3 | 14元 |
| 三月份 | 35m3 | 19元 |
| A. | 11.5元 | B. | 11元 | C. | 10.5元 | D. | 10元 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com