
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
分析 利用数量积运算性质、向量夹角公式、向量共线定理即可得出.
解答 解:$\overrightarrow{a}$,$\overrightarrow{b}$不共线的两个向量,若命题p:$\overrightarrow{a}•\overrightarrow{b}$>0,则$cos<\overrightarrow{a},\overrightarrow{b}>$>0?$\overrightarrow{a},\overrightarrow{b}$夹角是锐角,
因此命题p是命题q成立的充要条件.
故选:C.
点评 本题考查了数量积运算性质、向量夹角公式、向量共线定理、简易逻辑的判定方法,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2187 | C. | 2188 | D. | -2187 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
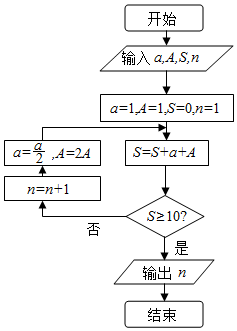 我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )
我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )| A. | 4 | B. | 5 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 1440 | C. | 720 | D. | 2160 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某公司要在一条笔直的道路边安装路灯,要求灯柱AB与地面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂,路灯C采用锥形灯罩,射出的光线与平面ABC的部分截面如图中阴影部分所示.已知∠ABC=$\frac{2}{3}$π,∠ACD=$\frac{π}{3}$,路宽AD=24米.设∠BAC=θ$(\frac{π}{12}≤θ≤\frac{π}{6})$
某公司要在一条笔直的道路边安装路灯,要求灯柱AB与地面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂,路灯C采用锥形灯罩,射出的光线与平面ABC的部分截面如图中阴影部分所示.已知∠ABC=$\frac{2}{3}$π,∠ACD=$\frac{π}{3}$,路宽AD=24米.设∠BAC=θ$(\frac{π}{12}≤θ≤\frac{π}{6})$查看答案和解析>>
科目:高中数学 来源: 题型:填空题
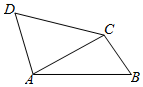 如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.
如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com