
分析 (1)直接取x1=1,x2=0,利用f(x1+x2)≥f(x1)+f(x2)可得:f(0)≤0,再结合已知条件f(0)≥0,即可求得f(0)=0.
(2)由0≤x1<x2≤1,则0<x1-x2<1,故有f(x2)=f(x2-x1+x2)≥f(x2-x1)+f(x1)≥f(x1),即f(x)在[0,1]内是增函数,故函数f(x)有最大值为f(1).
(3)①当x∈($\frac{1}{2},1$]时,f(x)≤1<2x,②当x∈(0,$\frac{1}{2}$]时,可知对于x∈$(\frac{1}{{2}^{n+1}},\frac{1}{{2}^{n}}]$,总有f(x)<$\frac{1}{{2}^{n}}$,其中n=1,2,…,而对于任意x∈$(0,\frac{1}{2}]$,存在正整数n,使得x∈($\frac{1}{{2}^{n+1}},\frac{1}{{2}^{n}}$],此时f(x)≤$\frac{1}{{2}^{n}}$≤2x,③当x=0时,f(0)=0≤2x所以,满足条件的函数f(x),对x∈[0,1],总有f(x)≤2x成立.
解答 解:(1)∵f(x1+x2)≥f(x1)+f(x2),
∴f(1+0)≥f(1)+f(0),
∴f(0)≤0,
∵?x∈[0,1],恒有f(x)≥0,
故f(0)=0.
(2)∵0≤x1<x2≤1,则0<x1-x2<1,
∴f(x2)=f(x2-x1+x2)≥f(x2-x1)+f(x1)≥f(x1),
故有f(x1)≤f(x2),
∴f(x)在[0,1]内是增函数,
于是当0≤x≤1时,有f(x)≤f(1)=1,
因此,当x=1时,f(x)有最大值为1;
(3)证明:研究①当x∈($\frac{1}{2},1$]时,f(x)≤1<2x,
②当x∈(0,$\frac{1}{2}$]时,
首先,f(2x)≥f(x)+f(x)=2f(x),
∴f(x)≤$\frac{1}{2}$f(2x),
显然,当x∈$(\frac{1}{{2}^{2}},\frac{1}{2}]$时,
f(x)≤f($\frac{1}{2}$)≤$\frac{1}{2}f(2\frac{1}{2})=\frac{1}{2}f(1)=\frac{1}{2}$成立,
假设当x$∈(\frac{1}{{2}^{k+1}},\frac{1}{{2}^{k}}]$时,有f(k)$≤\frac{1}{{2}^{k}}$成立,其中k=1,2,…,
那么当$x∈(\frac{1}{{2}^{k+2}},\frac{1}{{2}^{k+1}}]$时,
f(x)≤$f(\frac{1}{{2}^{k+1}})≤\frac{1}{2}f(2\frac{1}{{2}^{k+1}})$=
$\frac{1}{2}f(\frac{1}{{2}^{k}})≤\frac{1}{2}\frac{1}{{2}^{k}}=\frac{1}{{2}^{k+1}}$,
可知对于x∈$(\frac{1}{{2}^{n+1}},\frac{1}{{2}^{n}}]$,总有f(x)<$\frac{1}{{2}^{n}}$,其中n=1,2,…,
而对于任意x∈$(0,\frac{1}{2}]$,存在正整数n,使得x∈($\frac{1}{{2}^{n+1}},\frac{1}{{2}^{n}}$],
此时f(x)≤$\frac{1}{{2}^{n}}$≤2x,
③当x=0时,f(0)=0≤2x,
综上可知,满足条件的函数f(x),对x∈[0,1],总有f(x)≤2x成立.
点评 本题考查在新定义下对抽象函数进行考查,在做关于新定义的题目时,一定要先研究定义,在理解定义的基础上再做题,解题时要认真审题,注意数学归纳法的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}i$ | D. | $-\frac{1}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 月份 | 用气量 | 煤气费 |
| 一月份 | 4m3 | 4元 |
| 二月份 | 25m3 | 14元 |
| 三月份 | 35m3 | 19元 |
| A. | 11.5元 | B. | 11元 | C. | 10.5元 | D. | 10元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{3}{2}$ | B. | $\frac{3}{2}$ | C. | -6 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 百分制 | 85以及以上 | 70分到84分 | 60分到69分 | 60分以下 |
| 等级 | A | B | C | D |
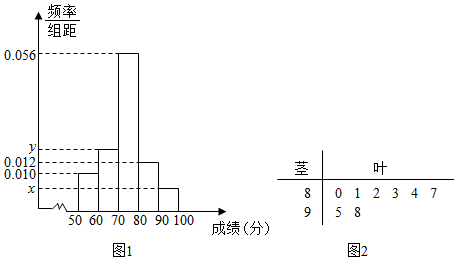
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com