
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 名题金卷系列答案
名题金卷系列答案科目:高中数学 来源: 题型:解答题
 某公司要在一条笔直的道路边安装路灯,要求灯柱AB与地面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂,路灯C采用锥形灯罩,射出的光线与平面ABC的部分截面如图中阴影部分所示.已知∠ABC=$\frac{2}{3}$π,∠ACD=$\frac{π}{3}$,路宽AD=24米.设∠BAC=θ$(\frac{π}{12}≤θ≤\frac{π}{6})$
某公司要在一条笔直的道路边安装路灯,要求灯柱AB与地面垂直,灯杆BC与灯柱AB所在的平面与道路走向垂,路灯C采用锥形灯罩,射出的光线与平面ABC的部分截面如图中阴影部分所示.已知∠ABC=$\frac{2}{3}$π,∠ACD=$\frac{π}{3}$,路宽AD=24米.设∠BAC=θ$(\frac{π}{12}≤θ≤\frac{π}{6})$查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{20}$ | B. | $\frac{1}{20}$ | C. | $\frac{5}{8}$ | D. | $\frac{2}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {-2} | B. | {-2,-1} | C. | {-2,-1,0} | D. | {0,1,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:
某赛季甲、乙两名篮球运动员每场比赛得分的原始记录如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
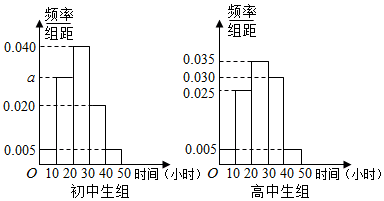
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com