
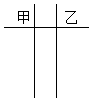
 ij�����ס������������˶�Աÿ�������÷ֵ�ԭʼ��¼���£�
ij�����ס������������˶�Աÿ�������÷ֵ�ԭʼ��¼���£����� ������ij�����ס������������˶�Աÿ�������÷ֵ�ԭʼ��¼���ó���Ҷͼ���ɾ�Ҷͼ�ã��ҵ�ƽ��ֵ���ڼ�ƽ�������ױ����ȶ���
����9�α����ĵ÷���ѡ2���÷֣������оٷ�����������÷ֶ�����25�ֵĸ��ʣ�
��� ��12�֣�
�⣺����Ҷͼ
�ɾ�Ҷͼ�ã��ҵ�ƽ��ֵ���ڼ�ƽ�������ױ����ȶ��� ����6�֣�
����9�α����ĵ÷���ѡ2���÷֣�����{34��21}��{34��13}��{34��30}��{34��29}��{34��33}��
{34��28}��{34��27}��{34��10}��{21��13}��{21��30}��{21��29}��{21��33}��{21��28}��{21��27}��
{21��10}��{13��30}��{13��29}��{13��33}��{13��28}��{13��27}��{13��10}��{30��29}��{30��33}��
{30��28}��{30��27}��{30��10}��{29��33}��{29��28}��{29��27}��{29��10}��{33��28}��{33��27}��
{33��10}��{28��27}��{28��10}��{27��10}����36�֣�
�÷ֶ�����25�ֵ���15�֣�
�������÷ֶ�����25�ֵĸ���p=$\frac{15}{36}$=$\frac{5}{12}$������12�֣�
���� ���⿼�龥Ҷͼ��������������ʵ����ǻ����⣬����ʱҪ�������⣬ע���оٷ��ĺ������ã�


 Ʒѧ˫�ž�ϵ�д�
Ʒѧ˫�ž�ϵ�д� Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
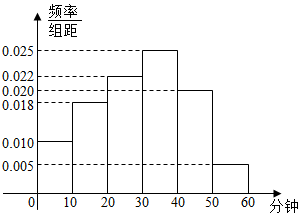 ijУΪ�˽ⱾУѧ���Ŀκ��������Ϸʱ������������ȡ��100��ѧ�����е��飮��ͼ�Ǹ��ݵ��������Ƶ�ѧ��ÿ���������Ϸ��ʱ����Ƶ�ʷֲ�ֱ��ͼ��
ijУΪ�˽ⱾУѧ���Ŀκ��������Ϸʱ������������ȡ��100��ѧ�����е��飮��ͼ�Ǹ��ݵ��������Ƶ�ѧ��ÿ���������Ϸ��ʱ����Ƶ�ʷֲ�ֱ��ͼ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2}$ | B�� | 1 | C�� | 2 | D�� | $\sqrt{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{5}{13}$ | B�� | -$\frac{5}{13}$ | C�� | $\frac{12}{13}$ | D�� | -$\frac{12}{13}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com