
| A. | $\frac{7}{20}$ | B. | $\frac{1}{20}$ | C. | $\frac{5}{8}$ | D. | $\frac{2}{7}$ |
分析 设事件A表示“考生甲在答对第一道题”,事件B表示“考生甲在答对第二道题”,由已知得P(B|A)=0.8,P(AB)=0.5,由此利用条件概率计算公式能求出考生甲答对第一道题的概率.
解答 解:设事件A表示“考生甲在答对第一道题”,事件B表示“考生甲在答对第二道题”,
∵某次招聘考试中,考生甲在答对第一道题的情况下也答对第二道题的概率为0.8,
这两道题均答对的概率为0.5,
∴P(B|A)=0.8,P(AB)=0.5,
∵P(B|A)=$\frac{P(AB)}{P(A)}$,
∴考生甲答对第一道题的概率:P(A)=$\frac{P(AB)}{P(B|A)}$=$\frac{0.5}{0.8}$=$\frac{5}{8}$.
故选:C.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意条件概率计算公式的合理运用.


科目:高中数学 来源: 题型:解答题
| 每周参与运动的时间(单位:小时) | [0,4) | [4,8) | [8,12) | [12,16) | [16,20] |
| 频数 | 24 | 40 | 28 | 6 | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
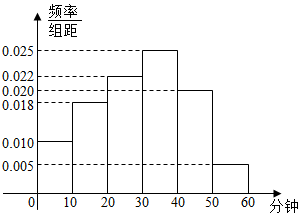 某校为了解本校学生的课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.如图是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.
某校为了解本校学生的课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.如图是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(2-\sqrt{3},2+\sqrt{3})$ | B. | $[2-\sqrt{3},2+\sqrt{3}]$ | C. | $(-∞,2-\sqrt{3})∪(2+\sqrt{3},+∞)$ | D. | $(-∞,2-\sqrt{3}]∪[2+\sqrt{3},+∞)$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com