
| A. | $(2-\sqrt{3},2+\sqrt{3})$ | B. | $[2-\sqrt{3},2+\sqrt{3}]$ | C. | $(-∞,2-\sqrt{3})∪(2+\sqrt{3},+∞)$ | D. | $(-∞,2-\sqrt{3}]∪[2+\sqrt{3},+∞)$ |
分析 求出圆的圆心与半径,利用圆心到直线的距离与半径的关系列出不等式求解即可.
解答 解:圆x2+y2-4x-4y-10=0整理为${(x-2)^2}+{(y-2)^2}={(3\sqrt{2})^2}$,
∴圆心坐标为(2,2),半径为3$\sqrt{2}$,要求圆上至少有三个不同的点到直线l:y=kx的距离为$2\sqrt{2}$,则圆心到直线的距离应不大于等于$\sqrt{2}$,∴$\frac{|2-2k|}{{\sqrt{1+{k^2}}}}≤\sqrt{2}$,∴$2-\sqrt{3}≤k≤2+\sqrt{3}$,
故选:B.
点评 本题考查直线与圆的位置关系的综合应用,考查计算能力以及转化思想的应用.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{20}$ | B. | $\frac{1}{20}$ | C. | $\frac{5}{8}$ | D. | $\frac{2}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
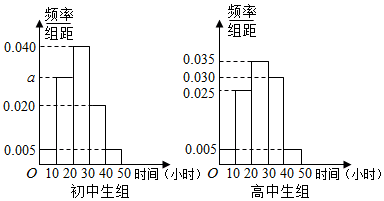
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{7}{2}$ | B. | $\frac{7}{2}$ | C. | $-\frac{7}{2}i$ | D. | $\frac{7}{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “p∨q为真”是“p∧q为真”的充分不必要条件 | |
| B. | 若a,b∈[0,1],则不等式a2+b2<$\frac{1}{4}$成立的概率是$\frac{1}{4}$ | |
| C. | 已知随机变量X~N(2,σ2),且P(X≤4)=0.84,则P(X≤0)=0.16 | |
| D. | 已知空间直线a,b,c,若a⊥b,b⊥c,则a∥c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com