
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
分析 由题意得取出的球的最大编号X的可能取值为2,3,分别求出相应的概率,由此能求出取出的球的最大编号X的均值.
解答 解:∵口袋中有编号分别为1、2、3的三个大小和形状相同的小球,从中任取2个,
∴取出的球的最大编号X的可能取值为2,3,
P(X=2)=$\frac{{C}_{2}^{2}}{{C}_{3}^{2}}$=$\frac{1}{3}$,
P(X=3)=$\frac{{C}_{2}^{1}{C}_{1}^{1}}{{C}_{3}^{2}}$=$\frac{2}{3}$,
∴取出的球的最大编号X的均值EX=$2×\frac{1}{3}+3×\frac{2}{3}$=$\frac{8}{3}$.
故选:D.
点评 本题考查离散型随机变量的数学期望的求法,是基础题,解题时要认真审题,注意排列组合知识的合理运用.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:高中数学 来源: 题型:解答题
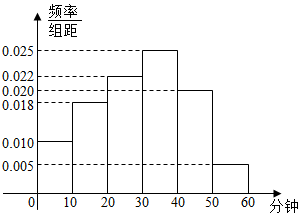 某校为了解本校学生的课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.如图是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.
某校为了解本校学生的课后玩电脑游戏时长情况,随机抽取了100名学生进行调查.如图是根据调查结果绘制的学生每天玩电脑游戏的时长的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $(2-\sqrt{3},2+\sqrt{3})$ | B. | $[2-\sqrt{3},2+\sqrt{3}]$ | C. | $(-∞,2-\sqrt{3})∪(2+\sqrt{3},+∞)$ | D. | $(-∞,2-\sqrt{3}]∪[2+\sqrt{3},+∞)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{13}$ | B. | -$\frac{5}{13}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com