
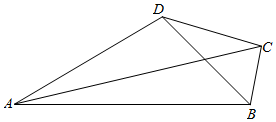
分析 (I)设∠ABD=α,∠CBD=β.在Rt△ABD中,cosα=$\frac{BD}{AB}$,可得α.在Rt△CBD中,cosβ=$\frac{BC}{BD}$,可得β.在△ABC中,利用余弦定理即可得出.
(II)设∠BDC=θ,在△ACD中,由正弦定理可得:$\frac{AC}{sin(9{0}^{°}+θ)}$=$\frac{2\sqrt{3}}{sin3{0}^{°}}$,化为AC=$4\sqrt{3}$cosθ.同理在△ABC中,利用正弦定理可得:AC=$\frac{8\sqrt{3}}{3}$cos(60°-θ),化简解出即可得出.
解答 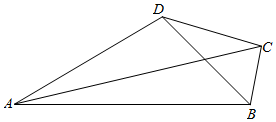 解:(I)设∠ABD=α,∠CBD=β
解:(I)设∠ABD=α,∠CBD=β
在Rt△ABD中,cosα=$\frac{BD}{AB}$=$\frac{2}{4}$=$\frac{1}{2}$,∴α=$\frac{π}{3}$.
在Rt△CBD中,cosβ=$\frac{BC}{BD}$=$\frac{1}{2}$,∴β=$\frac{π}{3}$.
∴α+β=$\frac{2π}{3}$.
在△ABC中,AC2=${1}^{2}+{4}^{2}-2×1×4×cos\frac{2π}{3}$=21.
∴AC=$\sqrt{21}$.
(II)设∠BDC=θ,在△ACD中,$\frac{AC}{sin(9{0}^{°}+θ)}$=$\frac{2\sqrt{3}}{sin3{0}^{°}}$,化为AC=$4\sqrt{3}$cosθ.
在△ABC中,$\frac{AC}{sin(6{0}^{°}+9{0}^{°}-θ)}$=$\frac{AB}{sin6{0}^{°}}$,化为:AC=$\frac{8\sqrt{3}}{3}$cos(60°-θ),
∴$4\sqrt{3}$cosθ═$\frac{8\sqrt{3}}{3}$cos(60°-θ),化为:3cosθ=2cos(60°-θ),
∴3cosθ=cosθ+$\sqrt{3}$sinθ,
∴tanθ=$\frac{2\sqrt{3}}{3}$.
点评 本题考查了正弦定理余弦定理的应用、直角三角形的边角关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | 2 | D. | $\frac{8}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
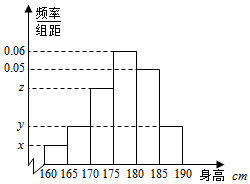 为了了解某中学男生身高,从该校的总共800名男生中抽取40名进行调查,并制成如下频率分布直方图,已知x:y:z=1:2:4.则y的值为0.02.
为了了解某中学男生身高,从该校的总共800名男生中抽取40名进行调查,并制成如下频率分布直方图,已知x:y:z=1:2:4.则y的值为0.02.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com