Question

12．下列程序输出的结果是（　　）

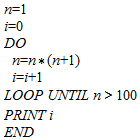
• A． 2
• B． 3
• C． 4
• D． 5

Answer 1

分析 模拟执行程序，依次写出每次循环得到的n，i的值，当n=1860时，满足条件n＞100，退出循环，输出i的值为4，从而得解．

解答 解：模拟执行程序，可得
n=1，i=0
执行循环体，n=1×2=2，i=1
不满足条件n＞100，执行循环体，n=2×3=6，i=2
不满足条件n＞100，执行循环体，n=6×7=42，i=3
不满足条件n＞100，执行循环体，n=42×43=1860，i=4
满足条件n＞100，退出循环，输出i的值为4．
故选：C．

点评 根据流程图（或伪代码）写程序的运行结果，是算法这一模块最重要的题型，其处理方法是：①分析流程图（或伪代码），从流程图（或伪代码）中既要分析出计算的类型，又要分析出参与计算的数据（如果参与运算的数据比较多，也可使用表格对数据进行分析管理）⇒②建立数学模型，根据第一步分析的结果，选择恰当的数学模型③解模．