
分析 (1)函数整理为y=mlnx+x,求导,由题意可知,函数的最小值应在极值点处取得,令f'(x)=$\frac{m}{x}$+1=0,代入求解即可;
(2)函数整理为g(x)=mlnx+mx2+(m2+2)x,求导得g'(x)=$\frac{(mx+1)(2x+m)}{x}$,对参数m进行分类讨论,逐一求出单调区间.
解答 解:(1)y=f(x)+x
=mlnx+x,
f'(x)=$\frac{m}{x}$+1=0,
∴m=-x0,
∵函数y=f(x)+x的最小值为0,
∴-x0lnx0+x0=0,
∴m=x0=$\frac{1}{e}$;
(2)g(x)=f(x)+mx2+(m2+2)x
=mlnx+mx2+(m2+2)x,
∴g'(x)=$\frac{(mx+1)(2x+m)}{x}$,
当m=0时,g(x)=2x,定义域内递增;
当m≠0时,
令g'(x)=0,
∴x=-$\frac{1}{m}$或x=-$\frac{m}{2}$
当m>0时,g'(x)>0,g(x)定义域内递增;
当m<0时,
当m>-$\sqrt{2}$时,函数的增区间为(0,-$\frac{m}{2}$)u(-$\frac{1}{m}$,+∞),减区间为(-$\frac{m}{2}$,-$\frac{1}{m}$);
当m<-$\sqrt{2}$时,函数的增区间为(0,-$\frac{1}{m}$)u(-$\frac{m}{2}$,+∞),减区间为(-$\frac{1}{m}$,-$\frac{m}{2}$);
当m=-$\sqrt{2}$时,定义域内递增.
点评 本题考查了利用导函数求函数的单调性问题,难点是对导函数中参数的讨论问题.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 钝角三角形 | B. | 锐角三角形 | C. | 等腰三角形 | D. | 直角三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
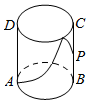 如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )
如图,有一圆柱形无盖水杯,其轴截面ABCD是边长为2的正方形,P是BC的中点,现有一只蚂蚁位于外壁A处,内壁P处有一粒米,则这只蚂蚁取得米粒所经过的最短路程是( )| A. | $\sqrt{5}$ | B. | π+1 | C. | $\sqrt{{π}^{2}+1}$ | D. | $\sqrt{{π}^{2}+9}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com