
 ij��˾Ҫ��һ����ֱ�ĵ�·�߰�װ·�ƣ�Ҫ�����AB����洹ֱ���Ƹ�BC�����AB���ڵ�ƽ�����·����·��C�����ε��֣�����Ĺ�����ƽ��ABC�IJ��ֽ�����ͼ����Ӱ������ʾ����֪��ABC=$\frac{2}{3}$�У���ACD=$\frac{��}{3}$��·��AD=24�ף����BAC=��$��\frac{��}{12}�ܦȡ�\frac{��}{6}��$
ij��˾Ҫ��һ����ֱ�ĵ�·�߰�װ·�ƣ�Ҫ�����AB����洹ֱ���Ƹ�BC�����AB���ڵ�ƽ�����·����·��C�����ε��֣�����Ĺ�����ƽ��ABC�IJ��ֽ�����ͼ����Ӱ������ʾ����֪��ABC=$\frac{2}{3}$�У���ACD=$\frac{��}{3}$��·��AD=24�ף����BAC=��$��\frac{��}{12}�ܦȡ�\frac{��}{6}��$���� ��1���ڡ�ACD�����ڡ�ABC�У��ֱ��������Ҷ������ɵó���
��2����ABC�У��������Ҷ����ɵã�BC�������úͲʽ���ɵó���
��� �⣺��1���ڡ�ACD�У�$��CDA=��+\frac{��}{6}$��
��$\frac{AD}{sin��ACD}=\frac{AC}{sin��CDA}$����$AC=\frac{AD•sin��CDA}{sin��ACD}=16\sqrt{3}sin����+\frac{��}{6}��$��
�ڡ�ABC�У�$��ACB=\frac{��}{3}-��$��
��$\frac{AB}{sin��ACB}=\frac{AC}{sin��ABC}$����$h=\frac{AC•sin��ACB}{sin��ABC}=32sin����+\frac{��}{6}��sin��\frac{��}{3}-�ȣ�$$��\frac{��}{12}�ܦȡ�\frac{��}{6}��$��
��2����ABC��
��$\frac{BC}{sin��BAC}=\frac{AC}{sin��ABC}$����$BC=\frac{AC•sin��BAC}{sin��ABC}=32sin����+\frac{��}{6}��sin��$��
��$AB+BC=32sin����+\frac{��}{6}��sin��\frac{��}{3}-�ȣ�+32sin����+\frac{��}{6}��sin��$=$16sin2��+8\sqrt{3}$��
��$\frac{��}{12}�ܦȡ�\frac{��}{6}$����$\frac{��}{6}��2�ȡ�\frac{��}{3}$��
�൱$��=\frac{��}{12}$ʱ��AB+BCȡ����Сֵ$8+8\sqrt{3}��21.86$��
������·�Ƶ���AB��Ƹ�BC���ò��ϵ��ܳ�����С����СֵԼΪ21.86�ף�
���� ���⿼�������Ҷ������Ҷ������Ͳʽ�����Ǻ�����ֵ��������������������������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
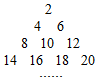 ����ż��������ͼ�����е�i�к͵�j�е�����ʾΪaij=��i��j��N+��������a43=18����aij=2016����i+j=63��
����ż��������ͼ�����е�i�к͵�j�е�����ʾΪaij=��i��j��N+��������a43=18����aij=2016����i+j=63���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ÿ�ܲ����˶���ʱ�䣨��λ��Сʱ�� | [0��4�� | [4��8�� | [8��12�� | [12��16�� | [16��20] |
| Ƶ�� | 24 | 40 | 28 | 6 | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��һ���� | B�� | �ڶ����� | C�� | �������� | D�� | �������� |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com