
分析 (1)需要特别注意构造方法,x=y•$\frac{x}{y}$即可.
(2)抽象函数的单调性证明需要特别注意构造方法,构造出$\frac{{x}_{1}}{{x}_{2}}$∈(0,1),可应用已知得f($\frac{{x}_{1}}{{x}_{2}}$)>0,进而根据函数单调性的定义得到结论.
(3)根据若f(3)=1,f(9)=2,根据运算法以及单调性求得a的范围.
解答 解:(1)证明:由题意得:
f(x)=f(y•$\frac{x}{y}$)=f(y)+f($\frac{x}{y}$),
故f($\frac{x}{y}$)=f(x)-f(y).
(2)证明:设0<x1<x2,
∴f(x1)=f(${x}_{2}•\frac{{x}_{1}}{{x}_{2}}$)=f(x2)+f($\frac{{x}_{1}}{{x}_{2}}$),
∵当x∈(0,1)时f(x)>0,
∵$\frac{{x}_{1}}{{x}_{2}}$∈(0,1),∴f($\frac{{x}_{1}}{{x}_{2}}$)>0,
∴f(x1)>f(x2),
∴函数f(x)在定义域(0,+∞)上为减函数;
(3)若f(3)=1,
∴f(9)=2,
∴f(a)<f(a-1)+f(9)=f(9(a-1)),
∴a>9(a-1),
∴1<a<$\frac{9}{8}$.
点评 本题考查抽象函数的运算法则以及单调性的证明和解不等式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P(B|A)<P(AB) | B. | P(B|A)=$\frac{P(B)}{P(A)}$是可能的 | ||
| C. | 0<P(B|A)<1 | D. | P(A|A)=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 1440 | C. | 720 | D. | 2160 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
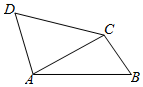 如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.
如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2$\sqrt{2}$) | B. | (-∞,2$\sqrt{2}$] | C. | (-∞,3) | D. | (-∞,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com