
| A. | ($\frac{e-1}{2}$,1)∪(1,e-1) | B. | ($\frac{e-1}{2}$,1)∪(1,e-1] | C. | ($\frac{e-1}{3}$,1)∪(1,e-1) | D. | ($\frac{e-1}{3}$,1)∪(1,e-1] |
分析 方程f(x)-mx-1=0恰有两个不同实根可转化为函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≤1}\\{f(x-2),x>1}\end{array}\right.$与直线y=mx+1的图象有且只有两个不同的交点,从而结合图象求解.
解答 解:∵方程f(x)-mx-1=0恰有两个不同实根,
∴函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≤1}\\{f(x-2),x>1}\end{array}\right.$与直线y=mx+1的图象有且只有两个不同的交点,
作函数f(x)=$\left\{\begin{array}{l}{{e}^{x},x≤1}\\{f(x-2),x>1}\end{array}\right.$与直线y=mx+1的图象如下,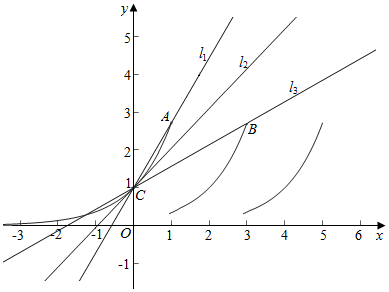
易知直线y=mx+1恒过点C(0,1),且点A(1,e),B(3,e);
故${k}_{{1}_{1}}$=kAC=$\frac{e-1}{1-0}$=e-1,${k}_{{l}_{3}}$=kBC=$\frac{e-1}{3-0}$=$\frac{e-1}{3}$;
f′(x)=ex,f′(0)=e0=1;
故${k}_{{l}_{2}}$=1;
故结合函数的图象可知,
$\frac{e-1}{3}$<m<1或1<m≤e-1,
故选D.
点评 本题考查了方程的根与函数的零点的关系应用及数形结合的思想应用,同时考查了分类讨论与转化思想的应用及导数的综合应用,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | P(B|A)<P(AB) | B. | P(B|A)=$\frac{P(B)}{P(A)}$是可能的 | ||
| C. | 0<P(B|A)<1 | D. | P(A|A)=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
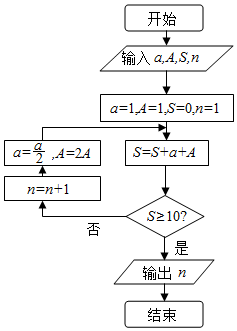 我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )
我国古代数学典籍《九章算术》“盈不足”中有一道两鼠穿墙问题:“今有垣厚十尺,两鼠对穿,初日各一尺,大鼠日自倍,小鼠日自半,问几何日相逢?”现用程序框图描述,如图所示,则输出结果n=( )| A. | 4 | B. | 5 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 50 | B. | 1440 | C. | 720 | D. | 2160 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
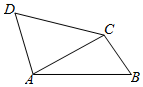 如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.
如图,△ABC中,AB=4,BC=2,∠ABC=∠D=60°,△ADC是锐角三角形,DA+DC的取值范围为$(6,4\sqrt{3}]$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com