
| A. | (-∞,-1] | B. | (-∞,$\sqrt{2}$] | C. | [-1,$\sqrt{2}$] | D. | [$\sqrt{2}$,+∞) |
分析 由题意可知:f(x)为R上的单调函数,则f(x)-2017x为定值,由指数函数的性质可知f(x)为R上的增函数,则g(x)在[-$\frac{π}{2}$,$\frac{π}{2}$]单调递增,求导,则g'(x)≥0恒成立,则k≤$\sqrt{2}$sin(x+$\frac{π}{4}$)min,根据函数的正弦函数的性质即可求得k的取值范围.
解答 解:若方程f'(x)=0无解,
则 f′(x)>0或f′(x)<0恒成立,所以f(x)为R上的单调函数,
?x∈R都有f[f(x)-2017x]=2017,
则f(x)-2017x为定值,
设t=f(x)-2017x,则f(x)=t+2017x,易知f(x)为R上的增函数,
∵g(x)=sinx-cosx-kx,
∴$g'(x)=cosx+sinx-k=\sqrt{2}sin({x+\frac{π}{4}})-k$,
又g(x)与f(x)的单调性相同,
∴g(x)在R上单调递增,则当x∈[-$\frac{π}{2}$,$\frac{π}{2}$],g'(x)≥0恒成立,
当$x∈[{-\frac{π}{2},\frac{π}{2}}]$时,$x+\frac{π}{4}∈[{-\frac{π}{4},\frac{3π}{4}}]$,$sin({x+\frac{π}{4}})∈[{-\frac{{\sqrt{2}}}{2},1}]$,
$\sqrt{2}sin({x+\frac{π}{4}})∈[{-1,\sqrt{2}}]$,
此时k≤-1,
故选A.
点评 本题考查导数的综合应用,考查利用导数求函数的单调性,正弦函数的性质,辅助角公式,考查计算能力,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $f(\frac{π}{2})>2f(\frac{π}{6})$ | B. | $\sqrt{3}f(\frac{π}{4})>\sqrt{2}f(\frac{π}{3})$ | C. | $\sqrt{3}f(\frac{π}{6})<f(\frac{π}{3})$ | D. | $f(1)<2f(\frac{π}{6})sin1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | a>c>b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
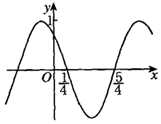 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )| A. | ω=π | |
| B. | φ=$\frac{π}{4}$ | |
| C. | f(x)的单调减区间为(2k-$\frac{1}{4}$,2k+$\frac{3}{4}$),k∈Z | |
| D. | f(x)的对称中心是(k+$\frac{1}{4}$,0),k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.
传承传统文化再掀热潮,央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏.将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级,随机从中抽取了100名选手进行调查,下面是根据调查结果绘制的选手等级人数的条形图.| 优秀 | 合格 | 合计 | |
| 大学组 | |||
| 中学组 | |||
| 合计 |
| P(k2≥k0) | 0.10 | 0.05 | 0.005 |
| k0 | 2.706 | 3.841 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 99 | B. | 90 | C. | 84 | D. | 70 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (2,+∞) | C. | (-∞,-6) | D. | (-6,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com