
【题目】设点P在曲线y=x2上,从原点向A(2,4)移动,如果直线OP,曲线y=x2及直线x=2所围成的面积分别记为S1、S2.
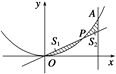
(1)当S1=S2时,求点P的坐标;
(2)当S1+S2有最小值时,求点P的坐标和最小值.
【答案】(1)![]() ,(2)
,(2)![]() ,
,![]()
【解析】
试题(1)可考虑用定积分求两曲线围成的封闭图形面积,直线OP的方程为y=tx,则S1为直线OP与曲线y=x2
当x∈(0,t)时所围面积,所以,S1=∫0t(tx﹣x2)dx,S2为直线OP与曲线y=x2当x∈(t,2)时所围面积,所以,
S2=∫t2(x2﹣tx)dx,再根据S1=S2就可求出t值.
(Ⅱ)由(2)可求当S1+S2,化简后,为t的三次函数,再利用导数求最小值,以及相应的x值,就可求出P点坐标为多少时,S1+S2有最小值.
试题解析:
(1)设点P的横坐标为t(0<t<2),则P点的坐标为(t,t2),
直线OP的方程为y=tx
S1=∫0t(tx﹣x2)dx=![]() ,S2=∫t2(x2﹣tx)dx=
,S2=∫t2(x2﹣tx)dx=![]() ,
,
因为S1=S2,,所以t=![]() ,点P的坐标为
,点P的坐标为![]()
(2)S=S1+S2=![]() =
=![]()
S′=t2﹣2,令S'=0得t2﹣2=0,t=![]()
因为0<t<![]() 时,S'<0;
时,S'<0;![]() <t<2时,S'>0
<t<2时,S'>0
所以,当t=![]() 时,Smin=
时,Smin=![]() ,P点的坐标为
,P点的坐标为![]() .
.


科目:高中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,椭圆![]()
![]() 的左焦点为
的左焦点为![]() ,右顶点为
,右顶点为![]() ,上顶点为
,上顶点为![]() .
.
(1)已知椭圆的离心率为![]() ,线段
,线段![]() 中点的横坐标为
中点的横坐标为![]() ,求椭圆的标准方程;
,求椭圆的标准方程;
(2)已知△![]() 外接圆的圆心在直线
外接圆的圆心在直线![]() 上,求椭圆的离心率
上,求椭圆的离心率![]() 的值.
的值.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知抛物线C:![]() ,过抛物线焦点F的直线交抛物线C于A,B两点,P是抛物线外一点,连接
,过抛物线焦点F的直线交抛物线C于A,B两点,P是抛物线外一点,连接![]() ,
,![]() 分别交抛物线于点C,D,且
分别交抛物线于点C,D,且![]() ,设
,设![]() ,
,![]() 的中点分别为M,N.
的中点分别为M,N.
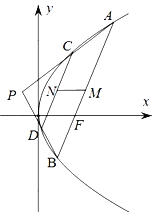
(1)求证:![]() 轴;
轴;
(2)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《算法统宗》全称《新编直指算法统宗》,是屮国古代数学名著,程大位著.书中有如下问题:“今有五人均银四十两,甲得十两四钱,戊得五两六钱.问:次第均之,乙丙丁各该若干?”意思是:有5人分40两银子,甲分10两4钱,戊分5两6钱,且相邻两项差相等,则乙丙丁各分几两几钱?(注:1两等于10钱)( )
A.乙分8两,丙分8两,丁分8两B.乙分8两2钱,丙分8两,丁分7两8钱
C.乙分9两2钱,丙分8两,丁分6两8钱D.乙分9两,丙分8两,丁分7两
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在棱长为1的正方体![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点.
的中点.![]() 为面对角线
为面对角线![]() 上任一点,则下列说法正确的是( )
上任一点,则下列说法正确的是( )

A.平面![]() 内存在直线与
内存在直线与![]() 平行
平行
B.平面![]() 截正方体
截正方体![]() 所得截面面积为
所得截面面积为![]()
C.直线![]() 和
和![]() 所成角可能为60°
所成角可能为60°
D.直线![]() 和
和![]() 所成角可能为30°
所成角可能为30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 过点
过点![]() ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知圆方程为![]() ,过圆上任意一点作圆的切线,切线与椭圆
,过圆上任意一点作圆的切线,切线与椭圆![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 为坐标原点,设
为坐标原点,设![]() 为
为![]() 的中点,求
的中点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
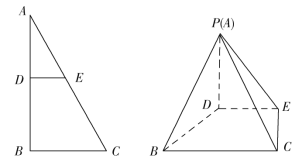
如图,已知![]() 是以
是以![]() 的直角三角形铁皮,
的直角三角形铁皮,![]() 米,
米,![]() 分别是边
分别是边![]() 上不与端点重合的动点,且
上不与端点重合的动点,且![]() .现将
.现将![]() 铁皮沿
铁皮沿![]() 折起至
折起至![]() 的位置,使得平面
的位置,使得平面![]() 平面
平面![]() ,连接
,连接![]() ,如图所示.现要制作一个四棱锥
,如图所示.现要制作一个四棱锥![]() 的封闭容器,其中
的封闭容器,其中![]() 铁皮和直角梯形
铁皮和直角梯形![]() 铁皮分别是这个封闭容器的一个侧面和底面,其他三个侧面用相同材料的铁皮无缝焊接密封而成(假设制作过程中不浪费材料,且铁皮厚度忽略不计).
铁皮分别是这个封闭容器的一个侧面和底面,其他三个侧面用相同材料的铁皮无缝焊接密封而成(假设制作过程中不浪费材料,且铁皮厚度忽略不计).
(1)若![]() 为
为![]() 边的中点,求制作三个新增侧面的铁皮面积是多少平方米?
边的中点,求制作三个新增侧面的铁皮面积是多少平方米?
(2)求这个封闭容器的最大体积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com