
【题目】为响应党中央“扶贫攻坚”的号召,某单位指导一贫困村通过种植紫甘薯来提高经济收入.紫甘薯对环境温度要求较高,根据以往的经验,随着温度的升高,其死亡株数成增长的趋势.下表给出了2018年种植的一批试验紫甘薯在不同温度时6组死亡的株数:
温度 | 21 | 23 | 24 | 27 | 29 | 32 |
死亡数 | 6 | 11 | 20 | 27 | 57 | 77 |
经计算:![]() ,
,![]() ,
,![]() ,
,![]() .
.
其中![]() 分别为试验数据中的温度和死亡株数,
分别为试验数据中的温度和死亡株数,![]() .
.
(1)![]() 与
与![]() 是否有较强的线性相关性? 请计算相关系数
是否有较强的线性相关性? 请计算相关系数![]() (精确到
(精确到![]() )说明.
)说明.
(2)并求![]() 关于
关于![]() 的回归方程
的回归方程![]() (
(![]() 和
和![]() 都精确到
都精确到![]() );
);
(3)用(2)中的线性回归模型预测温度为![]() 时该批紫甘薯死亡株数(结果取整数).
时该批紫甘薯死亡株数(结果取整数).
附:对于一组数据![]() ,
,![]() ,……,
,……,![]() ,
,
①线性相关系数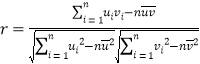 ,通常情况下当
,通常情况下当![]() 大于0.8时,认为两
大于0.8时,认为两
个变量有很强的线性相关性.
②其回归直线![]() 的斜率和截距的最小二乘估计分别为:
的斜率和截距的最小二乘估计分别为:
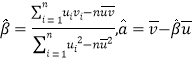 ;
;
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (a为实数).
(a为实数).
(1) 若函数![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 平行,求实数a的值;
平行,求实数a的值;
(2) 若![]() ,求函数
,求函数![]() 在区间
在区间![]() 上的值域;
上的值域;
(3) 若函数![]() 在区间
在区间![]() 上是增函数,求a的取值范围.
上是增函数,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数列![]() 的前
的前![]() 项和为
项和为![]() ,若数列
,若数列![]() 的各项按如下规律排列;
的各项按如下规律排列;![]() 有如下运算结论:①
有如下运算结论:①![]() ;②数列
;②数列![]() 是等比数列;③数列
是等比数列;③数列![]() 的前
的前![]() 项和为
项和为![]() ;④若存在正整数
;④若存在正整数![]() ,使得
,使得![]() ,则
,则![]() ,
,
其中正确的结论是________(将你认为正确的结论序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“把你的心我的心串一串,串一株幸运草串一个同心圆…”一位数学老师一这句歌词为灵感构造了一道名为《爱2017》的题目,请你解答此题:设O为坐标原点,直线l与圆C1:x2+y2=1相切且与圆C2:x2+y2=r2(r>1)相交于A、B两不同点,已知![]() E(x1,y1)、F(x2,y2)分别是圆C1、圆C2上的点.
E(x1,y1)、F(x2,y2)分别是圆C1、圆C2上的点.
(1)求r的值;
(2)求△OEF面积的最大值;
(3)若△OEF的外接圆圆心P在圆C1上,已知点D(3,0),求|DE|2+|DF|2的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=|x﹣a|+|x+5﹣a|
(1)若不等式f(x)﹣|x﹣a|≤2的解集为[﹣5,﹣1],求实数a的值;
(2)若x0∈R,使得f(x0)<4m+m2 , 求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() ,
, ![]() ,则实数
,则实数![]() 的取值范围为__________.
的取值范围为__________.
【答案】![]()
【解析】当m=0时,符合题意。
当m≠0时, ![]() ,则0<m<4,
,则0<m<4,
则0m<4
答案为: ![]() .
.
点睛:解本题的关键是处理二次函数在区间上大于0的恒成立问题,对于二次函数的研究一般从以几个方面研究:
一是,开口;
二是,对称轴,主要讨论对称轴与区间的位置关系;
三是,判别式,决定于x轴的交点个数;
四是,区间端点值.
【题型】填空题
【结束】
15
【题目】已知椭圆![]() :
: ![]() 的右焦点为
的右焦点为![]() ,
, ![]() 为直线
为直线![]() 上一点,线段
上一点,线段![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() :实数
:实数![]() 满足
满足![]() ,其中
,其中![]() ;命题
;命题![]() :方程
:方程![]() 表示双曲线.
表示双曲线.
(1)若![]() ,且
,且![]() 为真,求实数
为真,求实数![]() 的取值范围;
的取值范围;
(2)若![]() 是
是![]() 的充分不必要条件,求实数
的充分不必要条件,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:
先由命题解![]() 得
得![]() ;命题
;命题![]() 得
得![]() ,
,
(1)当![]() ,得命题
,得命题![]() ,再由
,再由![]() 为真,得
为真,得![]() 真且
真且![]() 真,即可求解
真,即可求解![]() 的取值范围.
的取值范围.
(2)由![]() 是
是![]() 的充分不必要条件,则
的充分不必要条件,则![]() 是
是![]() 的充分必要条件,根据则
的充分必要条件,根据则![]()
![]() ,即可求解实数
,即可求解实数![]() 的取值范围.
的取值范围.
试题解析:
命题![]() :由题得
:由题得![]() ,又
,又![]() ,解得
,解得![]() ;
;
命题![]() :
: ![]() ,解得
,解得![]() .
.
(1)若![]() ,命题
,命题![]() 为真时,
为真时, ![]() ,
,
当![]() 为真,则
为真,则![]() 真且
真且![]() 真,
真,
∴![]() 解得
解得![]() 的取值范围是
的取值范围是![]() .
.
(2)![]() 是
是![]() 的充分不必要条件,则
的充分不必要条件,则![]() 是
是![]() 的充分必要条件,
的充分必要条件,
设![]() ,
, ![]() ,则
,则![]()
![]() ;
;
∴![]() ∴实数
∴实数![]() 的取值范围是
的取值范围是![]() .
.
【题型】解答题
【结束】
19
【题目】已知抛物线顶点在原点,焦点在![]() 轴上,又知此抛物线上一点
轴上,又知此抛物线上一点![]() 到焦点的距离为6.
到焦点的距离为6.
(1)求此抛物线的方程;
(2)若此抛物线方程与直线![]() 相交于不同的两点
相交于不同的两点![]() 、
、![]() ,且
,且![]() 中点横坐标为2,求
中点横坐标为2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 为偶函数,求
为偶函数,求![]() 的值并写出
的值并写出![]() 的增区间;
的增区间;
(Ⅱ)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,当
,当![]() 时,求
时,求![]() 的最小值;
的最小值;
(Ⅲ)对任意的![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如果△A1B1C1的三个内角的余弦值分别等于△A2B2C2的三个内角的正弦值,则( )
A.△A1B1C1和△A2B2C2都是锐角三角形
B.△A1B1C1和△A2B2C2都是钝角三角形
C.△A1B1C1是钝角三角形,△A2B2C2是锐角三角形
D.△A1B1C1是锐角三角形,△A2B2C2是钝角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com