
【题目】古希腊毕达哥拉斯学派研究了“多边形数”,人们把多边形数推广到空间,研究了“四面体数”,下图是第一至第四个四面体数,(已知![]() )
)
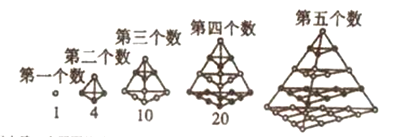
观察上图,由此得出第5个四面体数为______(用数字作答);第![]() 个四面体数为______.
个四面体数为______.
【答案】35 ![]()
【解析】
通过观察图形,先将图形的规律转化为数字规律,即为找到如1,4,10,20,……的数列的第![]() 项,通过观察发现,相邻的数字差分别是3,6,10,……,即第
项,通过观察发现,相邻的数字差分别是3,6,10,……,即第![]() 项应为
项应为![]() ,那么就把问题转化为求数列
,那么就把问题转化为求数列![]() 的和,
的和,![]() 为1,3,6,10,……,根据这些数字可以发现,
为1,3,6,10,……,根据这些数字可以发现,![]() ,
, ![]() ,……,
,……, ![]() ,利用累加法可以得到
,利用累加法可以得到![]() ,再利用题目所给已知,求出前
,再利用题目所给已知,求出前![]() 项和,即为第
项和,即为第![]() 个四面体数,当
个四面体数,当![]() 时,即为第5个四面体数.
时,即为第5个四面体数.
由题,
第一个四面体数为1;
第二个四面体数为![]() ;
;
第三个四面体数为![]() ;
;
第四个四面体数为![]()
……
由此可归纳,第![]() 个四面体数为
个四面体数为![]()
即为![]()
设该式中的每个数从左至右的排列为数列![]() ,即
,即![]() 为:1,3,6,10,……
为:1,3,6,10,……
得到递推关系为![]() ,
,![]() ,…,
,…,![]() ,相加后得
,相加后得![]()
![]() ,故数列
,故数列![]() 的和
的和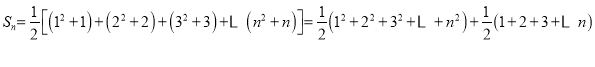
![]()
![]() 当
当![]() 时,
时,![]()
故答案为:35;![]()


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)求函数![]() 的最小正周期和单调递减区间;
的最小正周期和单调递减区间;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将所得图象的纵坐标不变,横坐标伸长到原来的2倍,得到的函数
个单位后,再将所得图象的纵坐标不变,横坐标伸长到原来的2倍,得到的函数![]() 的图象关于
的图象关于![]() 轴对称,求
轴对称,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数![]()
![]() ,有下列四个命题:①
,有下列四个命题:①![]() 的值域是
的值域是![]() ;②
;②![]() 是奇函数;③
是奇函数;③![]() 在
在![]() 上单调递增;④方程
上单调递增;④方程![]() 总有四个不同的解;其中正确的是( )
总有四个不同的解;其中正确的是( )
A.①②B.②③C.②④D.③④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 纸是生活中最常用的纸规格.
纸是生活中最常用的纸规格.![]() 系列的纸张规格特色在于:①
系列的纸张规格特色在于:①![]() 、
、![]() 、
、![]() 、…、
、…、![]() ,所有尺寸的纸张长宽比都相同.②在
,所有尺寸的纸张长宽比都相同.②在![]() 系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张
系列纸中,前一个序号的纸张以两条长边中点连线为折线对折裁剪分开后,可以得到两张后面序号大小的纸,比如1张![]() 纸对裁后可以的到2张
纸对裁后可以的到2张![]() 纸,1张
纸,1张![]() 纸对裁可以得到2张
纸对裁可以得到2张![]() 纸,以此类推.这是因为
纸,以此类推.这是因为![]() 系列的纸张长宽比为
系列的纸张长宽比为![]() 这一特殊比例,所以具备这种特性.已知
这一特殊比例,所以具备这种特性.已知![]() 纸规格为84.1厘米×118.9厘米(
纸规格为84.1厘米×118.9厘米(![]() ).那么
).那么![]() 纸的长度为( )
纸的长度为( )
A.14.8厘米B.21厘米C.25.1厘米D.29.7厘米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业准备招聘一批大学生到本单位就业,但在签约前要对他们的某项专业技能进行测试.在待测试的某一个小组中有男、女生共10人(其中女生人数多于男生人数),如果从中随机选2人参加测试,其中恰为一男一女的概率为![]() ;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为
;(Ⅰ)求该小组中女生的人数;(Ⅱ)假设此项专业技能测试对该小组的学生而言,每个女生通过的概率均为![]() ,每个男生通过的概率均为
,每个男生通过的概率均为![]() ;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量
;现对该小组中男生甲、男生乙和女生丙3个人进行测试,记这3人中通过测试的人数为随机变量![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,长半轴长与短半轴长的比值为
,长半轴长与短半轴长的比值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设经过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于不同的两点
相交于不同的两点![]() ,
,![]() .若点
.若点![]() 在以线段
在以线段![]() 为直径的圆上,求直线
为直径的圆上,求直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com