考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,不等式的证明
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,利用函数最值和导数之间的关系,即可求函数h(x)的最小值.
(Ⅱ)当a=-1时,根据函数h(x)=x2-lnx的单调性,利用函数单调性的性质即可证明不等式.
解答:
解:(Ⅰ)当x≤0时,函数h(x)=x
2单调递减,
所以函数h(x)在(-∞,0]上的最小值为h(0)=0
当x>0,h(x)=x
2+alnx
若a=0,函数h(x)=x
2在(0,+∞)上单调递
此时,函数h(x)不存在最小值
若a>0,因为
h′(x)=2x+=>0所以函数h(x)=x
2+alnx在(0,+∞)上单调递增
此时,函数h(x)不存在最小值
若a<0,因为
h′(x)==所以函数h(x)=x
2+alnx在
(0,)上单调递减
在
(,+∞)上单调递增
此时,函数h(x)的最小值为
h()因为
h()=-+aln=-+ln(-)=-[1-ln(-)]所以当-2e≤a<0时,
h()≥0当a<-2e时,
h()<0综上可知,当a>0时,函数h(x)没有最小值
当-2e≤a<0时,函数h(x)的最小值为h(0)=0
当a<-2e时,函数h(x)的最小值为
h()=-[1-ln(-)](Ⅱ)当a=-1时,由(Ⅱ)知h(x)=x
2-lnx在(1,+∞)为增函数?x>1,h(x)>h(1)=1,
所以x
2-lnx>1>0,即x
2>lnx
令
x==1+>1,
所以
()2>ln(),
所以
+++…+>ln(…)=ln(n+1).
点评:本题主要考查函数单调性最值和导数之间的关系,以及利用导数证明不等式,综合性较强,难度较大.



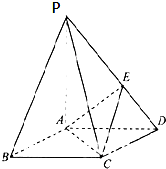 如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=
如图,在底面为菱形的四棱锥P-ABCD中,∠ABC=60°,PA=AC=1,PB=PD=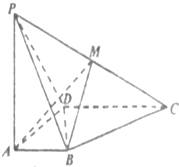 如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.
如图所示,四棱锥P-ABCD中,AB⊥AD,CD⊥AD,PA⊥底面ABCD,PA=AD=CD=2AB=2,M为PC的中点.