
分析 考查放缩法的运用.首先应明确由a2015的范围,求得a2016的范围,可以确定a2015∈(3,4),进而可得a2016的范围,即可求得k的值.
解答 解:∵an+1=lg(n+1+an),n∈N*,
取n=2014,∴a2015=lg(2015+a2014)>lg2015>3,
∴a2016=lg(2016+a2015)>lg(2016+3)=lg2019,
又数列{an}满足a1=0,an+1=lg(n+1+an),n∈N*,
∴a2=lg2<4,a3=lg(3+a2)<4,…,a2014=lg(2014+a2013)<4,
∴a2015<lg(2015+4)<4,
∴a2016<lg(2016+4)=lg2020,
综上,a2016∈(lg2019,lg2020),
∵a2016∈(lgk,lg(k+1)),
∴k=2019,
故答案为:2019.
点评 本题考查数列递推式,考查放缩法的运用,考查学生的计算能力,有难度.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
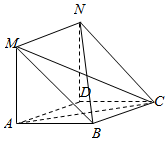 如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形.已知MA=3,AD=4,∠BAD=60°.
如图,在菱形ABCD中,MA⊥平面ABCD,且四边形ADNM是平行四边形.已知MA=3,AD=4,∠BAD=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2和5 | B. | 5和6 | C. | 2和11 | D. | 6和11 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
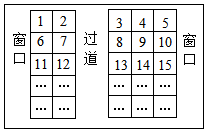 两同学预定春节返程票,希望两座相连,且有一人靠窗,从网上看余票尚有(48,49)、(62,63)、(75,76)、(84,85)四组,硬座车厢的座位号设置如图所示,那么他们应该订购的座位号是(84,85).
两同学预定春节返程票,希望两座相连,且有一人靠窗,从网上看余票尚有(48,49)、(62,63)、(75,76)、(84,85)四组,硬座车厢的座位号设置如图所示,那么他们应该订购的座位号是(84,85).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题①,②均为真命题 | B. | 命题②,③均为假命题 | ||
| C. | 命题②,④均为假命题 | D. | 命题①,③,④均为真命题 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com