
分析 (Ⅰ)求出圆心与半径,可得圆C的方程,再分类讨论,设出切线方程,利用直线是切线建立方程,即可得出结论;
(Ⅱ)先确定P的轨迹方程,再利用要使|PM|最小,只要|PO|最小即可.
解答 解:(Ⅰ)∵点P1(-2,3),P2(0,1),圆C是以P1P2的中点为圆心,$\frac{1}{2}$|P1P2|为半径的圆
∴C(-1,2),$\frac{1}{2}$|P1P2|=$\sqrt{2}$
∴圆C的方程为(x+1)2+(y-2)2=2,
当切线过原点时,设切线方程为y=kx,则$\frac{|k+2|}{\sqrt{{k}^{2}+1}}$=$\sqrt{2}$,
∴k=2±$\sqrt{6}$,即切线方程为y=(2±$\sqrt{6}$)x.
当切线不过原点时,设切线方程为x+y=a,则$\frac{|-1+2-a|}{\sqrt{2}}$=$\sqrt{2}$,
∴a=-1或a=3,即切线方程为x+y+1=0或x+y-3=0.
综上知,切线方程为y=(2±$\sqrt{6}$)x或x+y+1=0或x+y-3=0;
(Ⅱ)因为|PO|2+r2=|PC|2,所以x12+y12+2=(x1+1)2+(y1-2)2,即2x1-4y1+3=0.
要使|PM|最小,只要|PO|最小即可.
当直线PO垂直于直线2x-4y+3=0时,即直线PO的方程为2x+y=0时,|PM|最小,
此时P点即为两直线的交点,得P点坐标(-$\frac{3}{10}$,$\frac{3}{5}$).
点评 本题考查直线与圆的位置关系,考查学生分析解决问题的能力,考查学生的计算能力,考查分类讨论的数学思想,属于中档题.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:高中数学 来源: 题型:解答题
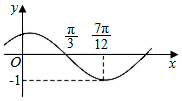 函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如图所示.
函数f(x)=Asin(ωx+φ)(其中A>0,ω>0,0<φ<$\frac{π}{2}$)的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
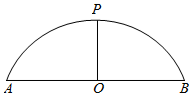 如图是某圆拱桥的示意图.这个圆拱桥的水面跨度AB=24m,拱高OP=8m.现有一船,宽10m,水面以上高6m,这条船能从桥下通过吗?为什么?
如图是某圆拱桥的示意图.这个圆拱桥的水面跨度AB=24m,拱高OP=8m.现有一船,宽10m,水面以上高6m,这条船能从桥下通过吗?为什么?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com