
分析 (Ⅰ)由题意求得tanα=3,再利用同角三角函数的基本关系化简所给的式子,可得结果.
(Ⅱ)利用同角三角函数的基本关系、二倍角公式化简所给的式子,可得结果.
解答 解:(Ⅰ)∵$\frac{4sinα-2cosα}{5cosα+3sinα}$=$\frac{4tanα-2}{5+3tanα}$=$\frac{5}{7}$,∴tanα=3,
∴sinα•cosα=$\frac{sinα•cosα}{si{n}^{2}α+co{s}^{2}α}$=$\frac{tanα}{ta{n}^{2}α+1}$=$\frac{3}{{3}^{2}+1}$=$\frac{3}{10}$.
( II)$\frac{\sqrt{1-2sin10°cos10°}}{cos10°-\sqrt{1-co{s}^{2}170°}}$=$\frac{|cos10°-sin10°|}{cos10°-sin10°}$=1.
点评 本题主要考查同角三角函数的基本关系、二倍角公式的应用,属于基础题.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
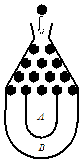 将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中它将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.
将一个半径适当的小球放入如图所示的容器最上方的入口处,小球将自由下落.小球在下落过程中它将3次遇到黑色障碍物,最后落入A袋或B袋中.已知小球每次遇到黑色障碍物时,向左、右两边下落的概率都是$\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com