
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①②③ |
分析 z1与z2是共轭虚数,设z1=a+bi(a,b∈R),z2=a-bi.利用复数的运算性质及其有关概念即可得出.
解答 解:z1与z2是共轭虚数,设z1=a+bi,z2=a-bi(a,b∈R).
命题①z12<|z2|2; ${z}_{1}^{2}$=a2-b2+2abi,复数不能比较大小,因此不正确;
②z1z2=|z1z2|=a2+b2,正确;
③z1+z2=2a∈R,正确;
④$\frac{{z}_{1}}{{z}_{2}}$=$\frac{a+bi}{a-bi}$=$\frac{(a+bi)^{2}}{(a-bi)(a+bi)}$=$\frac{{a}^{2}-{b}^{2}}{{a}^{2}+{b}^{2}}$+$\frac{2ab}{{a}^{2}+{b}^{2}}$i不一定是实数,因此不一定正确.
故选:B.
点评 本题考查了复数的运算法则、共轭复数的定义、模的计算公式,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
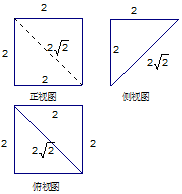
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{8\sqrt{2}}{3}$ | D. | $\frac{4\sqrt{2}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$] | B. | (1,+∞) | C. | (1,$\frac{9}{10}$+$\frac{ln2}{5}$) | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ex2-ex1>lnx2-lnx1 | B. | ex2-ex1<lnx2-lnx1 | ||
| C. | x2ex1>x1ex2 | D. | x2ex1<x1ex2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -4 | C. | -2$\sqrt{5}$ | D. | -3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com