
分析 根据题意,由于数列{an}具有性质P以及a2=a5=2,分析可得a3=a6=3,a4=a7,a5=a8=3,结合题意可以将a6+a7+a8=21变形为a3+a4+a5=21,计算可得a4的值,进而分析可得a3=a6=a9=…a3n=3,a4=a7=a6=…a3n+1=15,a5=a8=…a3n+2=3,(n≥1);分析可得a2017的值.
解答 解:根据题意,数列{an}具有性质P,且a2=a5=2,
则有a3=a6=3,a4=a7,a5=a8=3,
若a6+a7+a8=21,可得a3+a4+a5=21,则a4=21-3-3=15,
进而分析可得:a3=a6=a9=…a3n=3,a4=a7=a6=…a3n+1=15,a5=a8=…a3n+2=3,(n≥1)
则a2017=a3×672+1=15,
故答案为:15.
点评 本题考查数列的表示方法,关键分析什么样的数列具有性质P,并且求出a4的值,


科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ①②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
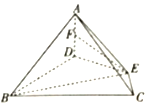 如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.
如图,在四棱锥A-BCED中,AD⊥底面BCED,BD⊥DE,∠DBC=∠BCE═60°,BD=2CE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{4}{5}$ | B. | $\frac{4}{5}$ | C. | -$\frac{4}{5}$i | D. | $\frac{4}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 40 | B. | 20 | C. | 31 | D. | 43 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-1,8) | B. | (0,5] | C. | [-1,5) | D. | (0,8) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com