
分析 (1)易知68-k(10-5)2+10=28,从而解得k=2;从而化简y=-2x3+33x2-108x-108(6<x<11);
(2)求导y′=-6(x-2)(x-9),从而判断函数的单调性,从而求最值.
解答 解:(1)∵m=68-k(x-5)2+x,
∴68-k(10-5)2+10=28,
解得,k=2;
∴m=68-2(x-5)2+x=-2x2+21x+18.
∴y=m(x-6)=(-2x2+21x+18)(x-6)
=-2x3+33x2-108x-108(6<x<11),
(2)由(1)知,y′=-6x2+66x-108=-6(x-2)(x-9),
令y′>0解得,6<x<9;令y′<0解得,9<x<11;
故y=-2x3+33x2-108x-108在(6,9)上单调递增,在(9,11)上单调递减;
故x=9时,年利润最大,最大为135万元.
答:售价为9元时,该吉祥物年利润最大,且最大年利润为135万元.
点评 本题考查了导数的综合应用及导数在实际问题中的应用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {2,3} | C. | {0,1} | D. | {2,3,4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22 | B. | 33 | C. | 44 | D. | 55 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{3}{8}$ | C. | $\frac{1}{2}$ | D. | $\frac{5}{8}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
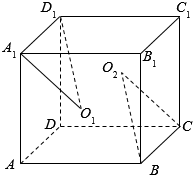 如图,在正方体ABCD-A1B1C1D1,O1,O2分别是正方形ABB1A1、DCC1D1的对角线的交点,求证:∠A1O1D1=∠CO2B.
如图,在正方体ABCD-A1B1C1D1,O1,O2分别是正方形ABB1A1、DCC1D1的对角线的交点,求证:∠A1O1D1=∠CO2B.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com